Projection to latent pathways (PLP): a constrained projection to latent variables (PLS) method for elementary flux modes discrimination

Abstract

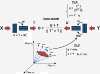
Background: Elementary flux modes (EFM) are unique and non-decomposable sets of metabolic reactions able to operate coherently in steady-state. A metabolic network has in general a very high number of EFM reflecting the typical functional redundancy of biological systems. However, most of these EFM are either thermodynamically unfeasible or inactive at pre-set environmental conditions.

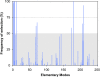
Results: Here we present a new algorithm that discriminates the "active" set of EFM on the basis of dynamic envirome data. The algorithm merges together two well-known methods: projection to latent structures (PLS) and EFM analysis, and is therefore termed projection to latent pathways (PLP). PLP has two concomitant goals: (1) maximisation of correlation between EFM weighting factors and measured envirome data and (2) minimisation of redundancy by eliminating EFM with low correlation with the envirome.

Conclusions: Overall, our results demonstrate that PLP slightly outperforms PLS in terms of predictive power. But more importantly, PLP is able to discriminate the subset of EFM with highest correlation with the envirome, thus providing in-depth knowledge of how the environment controls core cellular functions. This offers a significant advantage over PLS since its abstract structure cannot be associated with the underlying biological structure.

Figure 1

Schematic representation of decomposition operations performed by PLS and PLP algorithms. The main differences between PLS and PLP are related to the computation of Y-loadings. In PLS Q are abstract variables calculated to maximise correlation between X and Y, while in PLP Q comprises a subset of active EFM.

Figure 2

Correlation between EFM weighting factors and envirome variables. Observed weighting factors are plotted against a linear function of 26 envirome variables for the BHK data set. Blue circles and red triangles represent the calibration and validation data points, respectively.

Figure 3

Frequency of selection of EFM. A bootstrapping technique was implemented in which 200 PLP runs are performed for randomly selected calibration and validation data sets with 67 points each. Frequency is calculated as the EFM selection count divided by the total number of runs.

Figure 4

Normalized PLS output loadings versus reaction weighting factors of selected EFM. Blue circles and red triangles represent the loadings of the first and second PLS latent variable plotted against the corresponding metabolic reaction weighting factor of the first and second selected EFM (EFM179 and EFM1 respectively; see Tables 2 and 3).

Figure 5

PLP regression coefficients. Regression coefficients of selected EFM quantify the contribution of each environmental factor in X to the respective EFM weighting factor.

Figure 6

Regression coefficients confidence intervals for EFM 1. Confidence interval as function of regression coefficients obtained for the product formation EFM (EFM 1). Black full circles are envirome factors. The light and dark blue regions correspond to confidence intervals higher than 50% and 100% of the nominal value of the regression coefficient, respectively.

Figure 7

Predicted metabolic fluxes by PLS. Predicted against measured fluxes computed by the PLS model for the BHK data set. Blue circles and red triangles represent the calibration and validation data points, respectively.

Figure 8

Predicted metabolic fluxes by PLP. Predicted against measured fluxes computed by the PLP model for the BHK data set. Blue circles and red triangles represent the calibration and validation data points, respectively.