Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2012 Jul;13(3):371-83.
doi: 10.1093/biostatistics/kxr032. Epub 2011 Oct 31.

Competing risks regression for clustered data

Bingqing Zhou  1 , Jason Fine, Aurelien Latouche, Myriam Labopin
Affiliations

Competing risks regression for clustered data

Bingqing Zhou et al. Biostatistics. 2012 Jul.

Abstract

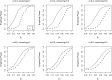
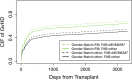
A population average regression model is proposed to assess the marginal effects of covariates on the cumulative incidence function when there is dependence across individuals within a cluster in the competing risks setting. This method extends the Fine-Gray proportional hazards model for the subdistribution to situations, where individuals within a cluster may be correlated due to unobserved shared factors. Estimators of the regression parameters in the marginal model are developed under an independence working assumption where the correlation across individuals within a cluster is completely unspecified. The estimators are consistent and asymptotically normal, and variance estimation may be achieved without specifying the form of the dependence across individuals. A simulation study evidences that the inferential procedures perform well with realistic sample sizes. The practical utility of the methods is illustrated with data from the European Bone Marrow Transplant Registry.

PubMed Disclaimer

Figures

Fig. 1.
Fig. 1.
The empirical powers of the tests for matched design.
Fig. 2.
Fig. 2.
The estimated cumulative incidence function.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Cai JW, Prentice RL. Regression estimation using multivariate failure time data and a common baseline hazard function model. Lifetime Data Analysis. 1997;3:197–213. - PubMed
    1. Chen BE, Kramer JL, Greene MH, Rosenberg PS. Competing risks analysis of correlated failure time data. Biometrics. 2008;64:172–179. - PMC - PubMed
    1. Clayton D, Cuzick J. Multivariate generalizations of the proportional hazards model. Journal of the Royal Statistical Society. Series A (General) 1985;148:82–117.
    1. Fine JP, Gray RJ. A proportional hazards model for the subdistribution of a competing risk. Journal of the American Statistical Association. 1999;94:496–509.
    1. Gray RJ. A class of K–sample tests for comparing the cumulative incidence of a competing risk. Annals of Statistics. 1988;16:1141–1154.

Publication types