A dynamical systems analysis of afferent control in a neuromechanical model of locomotion: II. Phase asymmetry

Abstract

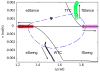
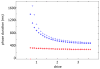
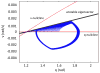
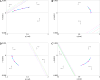
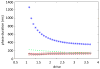
In this paper we analyze a closed loop neuromechanical model of locomotor rhythm generation. The model is composed of a spinal central pattern generator (CPG) and a single-joint limb, with CPG outputs projecting via motoneurons to muscles that control the limb and afferent signals from the muscles feeding back to the CPG. In a preceding companion paper (Spardy et al 2011 J. Neural Eng. 8 065003), we analyzed how the model generates oscillations in the presence or absence of feedback, identified curves in a phase plane associated with the limb that signify where feedback levels induce phase transitions within the CPG, and explained how increasing feedback strength restores oscillations in a model representation of spinal cord injury; from these steps, we derived insights about features of locomotor rhythms in several scenarios and made predictions about rhythm responses to various perturbations. In this paper, we exploit our analytical observations to construct a reduced model that retains important characteristics from the original system. We prove the existence of an oscillatory solution to the reduced model using a novel version of a Melnikov function, adapted for discontinuous systems, and also comment on the uniqueness and stability of this solution. Our analysis yields a deeper understanding of how the model must be tuned to generate oscillations and how the details of the limb dynamics shape overall model behavior. In particular, we explain how, due to the feedback signals in the model, changes in the strength of a tonic supra-spinal drive to the CPG yield asymmetric alterations in the durations of different locomotor phases, despite symmetry within the CPG itself.

Figure 1

Transitions between phases are marked over a range of drives. The solid arrows indicate the direction of increasing drive. Green circles denote the onset of fStance, magenta plus signs the onset of fSwing, black dots the onset of eSwing, and red stars the onset of eStance. The right hand side of the limb equation (1) changes in a discontinuous manner at each of these transitions. 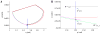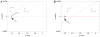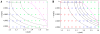A sample trajectory (for drive=1.4), which evolves in the clockwise direction as time advances, is plotted with a blue dashed line for reference, and the transition curves are plotted in black. Notice that the CPG transitions lie close to the TTC and WTC, respectively, though they are shifted due to the brief transient the model exhibits between phases (see [13], Appendix).

Figure 2

Motoneuron output generated by the original model (A) and reduced model (B) for drive strength d = 14. Red solid curves correspond to Mn - F, blue dashed to Mn - E. In the reduced model, motoneuron output is fixed at a different value in each phase, for each drive.

Figure 3

Reduced model preserves phase asymmetry as drive is increased. Stance and swing phase durations for the original model are shown in blue and red stars, respectively. Stance and swing phase durations for the reduced model are plotted in analogous colors with plus signs.

Figure 4

A general schematic of the set-up for the existence argument. We wish to show that as ε is increased from 0, the homoclinic perturbs as shown, so that trajectories are trapped in forward time within the region bounded by the unstable and stable manifolds of x_ε. Arrows indicate flow in the forward direction.

Figure 5

Key structures for the Melnikov argument for ε = 0.01 and 0.1 with $\{M_{\mathit{eSt}}^{\ast },M_{\mathit{fSt}}^{\ast },M_{\mathit{fSw}}^{\ast },M_{\mathit{eSw}}^{\ast }\}=\{67,-90,-100,-2.25\}$. (A) The closed orbit γ₀ for system (9) with ε = 0 is plotted with a blue dotted line, along with the manifolds W^u(x_ε) {red, black} and W̃^s(x_ε) {pink, green} for system (9) with ε ∈ {0.01, 0.1}. The transversal Σ is chosen as a vertical line (blue) through the point where eSwing begins on γ₀ (indicated with a blue star). (B) Zoomed view of (A) near the intersection of γ₀ and invariant manifolds with Σ, showing that W^u(x_ε) perturbs to the inside of W̃^s (x_ε) in both cases. For ε sufficiently close to 0, W̃^s(x_ε) remains close to γ₀, and it perturbs below γ₀ as ε increases. In (B), labeled manifolds and points indicate the ε = 0.1 case.

Figure 6

Strong contraction to the unstable manifold of the eStance critical point suggests that the periodic orbit resulting from the Melnikov calculation is unique. The eStance limb nullclines are shown in red and the unstable eigenvector with a black dotted line. A set of eStance initial conditions on the q-axis quickly converge toward the unstable eigenvector of the critical point located where the v-nullcline intersects the q-axis.

Figure 7

The alignment of the limb trajectory relative to the v-nullcline depends on phase. (A), (B), (C), and (D) display structures in (q, v) phase space in the eStance, fStance, fSwing, and eSwing phase, respectively, with panel ordering selected to reflect the order in which the phases occur, progressing clockwise. In each, the q-nullcline, which is the q-axis, is shown in black. A portion of the trajectory is plotted in blue, with different colored time points highlighted, and the same color is used for each corresponding v-nullcline, since the v-nullcline changes position over time as the output of the active motoneuron changes. Note that the v-nullcline positions differ drastically between phases, due to dominance switching in the CPG and the influence of ground contact.

Figure 8

Schematic illustration of the possible relationships the eStance v-nullcline can have with the limb trajectory at the onset of eStance. (A) The limb trajectory moves up and to the right through phase space when it enters eStance to the right of the eStance v-nullcline. (B) To the left of the v-nullcline, the vector field points down and to the right. Thus, the limb cannot proceed if it tries to enter eStance to the left of the eStance v-nullcline.

Figure 9

The location of the unstable eStance eigenvector determines the position where the limb trajectory crosses the TTC. Colored stars on the limb trajectory are plotted at various time points with their corresponding unstable eigenvector. The TTC is shown in magenta. (A) For a small drive value, hence, small Mn - E output, the unstable eigenvector lies at low velocities, and the trajectory lies very close to these eigenvectors until it crosses through the TTC. (B) For a large drive value, hence, large Mn - E output, the unstable eigenvector is far from the initial position the trajectory takes in eStance. The trajectory is pulled upwards toward the eigenvector and thus crosses the TTC at a higher velocity than in the small drive case.

Figure 10

The positions of the stable eigenvectors and the limb trajectory change with drive strength. (A) Small drive leads to small Mn - F output and stable eigenvectors that lie in a region of small positive velocity, but the limb trajectory enters this phase far below them. (B) Large drive, with large Mn - F output, yields stable eigenvectors shifted farther upward than in (A), such that trajectories with larger initial fStance velocities still lie below them. Time points on the limb trajectory are shown with stars, while the color-coordinated lines are the corresponding stable eigenvectors.

Figure 11

v̇ values at sample (q, v) points and level sets of L in the fSwing phase for small Mn - F (A) and large Mn - F (B). In both plots, black diamonds, green plus signs, magenta stars, blue circles, and red arrows correspond to v̇ values within (+/−) 5e-6 of −5e-5, −4e-5, −3e-5, −2e-5, and −1e-5, respectively. Level curves of L̂ are plotted in black, with smaller L̂ values closer to the q-axis, and the WTC is plotted in magenta. Initial conditions for this phase lie on the q-axis with varying angle. For the drive shown in (A), the oscillation trajectory would begin fStance closer to the WTC but travel more slowly than in (B), where the trajectory would enter fStance at a larger angle but travel faster. For constant Mn - F output, trajectories move in the direction of decreasing L̂.

Figure 12

v̇ values for a sample of (q, v) points and level curves in the eSwing phase for small Mn - E (A) and large Mn - E (B). Magenta plus signs, green stars, blue circles, and red diamonds correspond to v̇ values within (+/−) 5e-6 of 1e-5, 2e-5, 3e-5, 4e-5, and 5e-5, respectively. Level curves of L̄ are plotted in black and the WTC is plotted in magenta. Ignoring the transient, trajectories enter this phase on the WTC. In (A), trajectories begin closer to the q-axis but travel more slowly than in (B), where trajectories begin farther from the q axis, but travel faster. The slope of the level curves becomes steeper as drive increases; thus, there is a bound on how small the q values reached by large drive trajectories can be.

Figure 13

Durations of each of the four subphases are plotted against drive strength. The duration of eStance is shown in blue, fStance in black, fSwing in green, and eSwing in red. The phase asymmetry shown in [13] Figure 3 is almost entirely restricted to the eStance phase, due to the unique nullcline/trajectory alignment that occurs for small drive values.

Figure 14

Stance and swing durations for various ground reaction force magnitudes (M_GRmax) are plotted against drive. The stance durations for full, half, and no GRF are plotted in blue, green, and black, respectively. The swing durations are plotted in red, cyan, and magenta and the resulting curves lie on top of each other. By reducing the impact of the ground strike force, the dependence of stance duration on drive (upper curves) is lost. The swing durations (lower curves) remain unaffected by this change.

Figure 15

Relationship between the critical points for system (9) and the angle upper bound, q̂. The critical points are plotted as blue asterisks on {v = 0} with an arrow indicating the trend in their location as ε increases, and the line {q = q̂} is indicated in red. The q and v-nullclines are plotted as black solid lines, and the stable manifold is a green dashed line for the ε = 1 system; these intersect in the rightmost critical point. For reference, the limit cycle for the ε = 1 system is plotted. In order to transition to the fSwing phase, the q-values on the limit cycle in fStance must be bounded above by the q-coordinates of the fStance critical point. q̂ was chosen as an upper bound of these bounds, so that M̂_F is an upper bound of M_F (q, v, m_fSt).