COORDINATE DESCENT ALGORITHMS FOR NONCONVEX PENALIZED REGRESSION, WITH APPLICATIONS TO BIOLOGICAL FEATURE SELECTION

Abstract

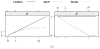
A number of variable selection methods have been proposed involving nonconvex penalty functions. These methods, which include the smoothly clipped absolute deviation (SCAD) penalty and the minimax concave penalty (MCP), have been demonstrated to have attractive theoretical properties, but model fitting is not a straightforward task, and the resulting solutions may be unstable. Here, we demonstrate the potential of coordinate descent algorithms for fitting these models, establishing theoretical convergence properties and demonstrating that they are significantly faster than competing approaches. In addition, we demonstrate the utility of convexity diagnostics to determine regions of the parameter space in which the objective function is locally convex, even though the penalty is not. Our simulation study and data examples indicate that nonconvex penalties like MCP and SCAD are worthwhile alternatives to the lasso in many applications. In particular, our numerical results suggest that MCP is the preferred approach among the three methods.

Fig. 1

Shapes of the lasso, SCAD and MCP penalty functions. The panel on the left plots the penalties themselves, whereas the panel on the right plots the derivative of the penalty. Note that none of the penalties are differentiable at β_j = 0.

Fig. 2

Example MCP coefficient paths for simulated data where p > n. The shaded region is the region in which the objective function is not locally convex. Note that the solutions are continuous and stable in the locally convex regions, but discontinuous and erratic otherwise.

Fig. 3

Time required (in seconds) to fit the entire coefficient paths for linear and logistic regression, employing either the local linear approximation (LLA) algorithm or the coordinate descent (CD) algorithm. Both axes are on the log scale. Times displayed are averaged over 100 independently generated data sets. The coordinate descent algorithm is at least 100 times faster than the LLA algorithm at all points.

Fig. 4

Relative (to the lasso) mean squared error for MCP- and SCAD-penalized linear and logistic regression. MSE was calculated for each penalty on 100 independently generated data sets, and the ratio of the medians is plotted. MCP and SCAD greatly outperform lasso for large coefficients, but not necessarily for small coefficients.

Fig. 5

MCP coefficient paths for various values of γ for the two studies of Section 6. The shaded region depicts areas that are not locally convex, and a vertical line is drawn at the value of λ selected by BIC. For the sparse genetic association data, small values of γ produce the best fit; for the dense microarray data, large values are preferred.