Neural dynamics as sampling: a model for stochastic computation in recurrent networks of spiking neurons
- PMID: 22096452
- PMCID: PMC3207943
- DOI: 10.1371/journal.pcbi.1002211
Neural dynamics as sampling: a model for stochastic computation in recurrent networks of spiking neurons
Abstract
The organization of computations in networks of spiking neurons in the brain is still largely unknown, in particular in view of the inherently stochastic features of their firing activity and the experimentally observed trial-to-trial variability of neural systems in the brain. In principle there exists a powerful computational framework for stochastic computations, probabilistic inference by sampling, which can explain a large number of macroscopic experimental data in neuroscience and cognitive science. But it has turned out to be surprisingly difficult to create a link between these abstract models for stochastic computations and more detailed models of the dynamics of networks of spiking neurons. Here we create such a link and show that under some conditions the stochastic firing activity of networks of spiking neurons can be interpreted as probabilistic inference via Markov chain Monte Carlo (MCMC) sampling. Since common methods for MCMC sampling in distributed systems, such as Gibbs sampling, are inconsistent with the dynamics of spiking neurons, we introduce a different approach based on non-reversible Markov chains that is able to reflect inherent temporal processes of spiking neuronal activity through a suitable choice of random variables. We propose a neural network model and show by a rigorous theoretical analysis that its neural activity implements MCMC sampling of a given distribution, both for the case of discrete and continuous time. This provides a step towards closing the gap between abstract functional models of cortical computation and more detailed models of networks of spiking neurons.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
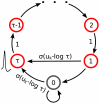
 for the internal state variable
for the internal state variable  of a spiking neuron
of a spiking neuron  with an absolute refractory period. The neuron can fire in the resting state
with an absolute refractory period. The neuron can fire in the resting state  and in the last refractory state
and in the last refractory state  .
.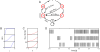
 , refractory functions
, refractory functions  and activation functions
and activation functions  for the neuron model with relative refractory mechanism. (A) Transition probabilities of the internal variable
for the neuron model with relative refractory mechanism. (A) Transition probabilities of the internal variable  given by
given by  . (B) Three examples of possible refractory functions
. (B) Three examples of possible refractory functions  . They assume value
. They assume value  when the neuron cannot spike, and return to value
when the neuron cannot spike, and return to value  (full readiness to fire again) with different time courses. The value of
(full readiness to fire again) with different time courses. The value of  at intermediate time points regulates the current probability of firing of neuron
at intermediate time points regulates the current probability of firing of neuron  (see A). The x-axis is equivalent to the number of time steps since last spike (running from 0 to
(see A). The x-axis is equivalent to the number of time steps since last spike (running from 0 to  from left to right). (C) Associated activation functions
from left to right). (C) Associated activation functions  according to (11). (D) Spike trains produced by the resulting three different neuron models with (hypothetical) membrane potentials that jump at time
according to (11). (D) Spike trains produced by the resulting three different neuron models with (hypothetical) membrane potentials that jump at time  from a constant low value to a constant high value. Black horizontal bars indicate spikes, and the active states
from a constant low value to a constant high value. Black horizontal bars indicate spikes, and the active states  are indicated by gray shaded areas of duration
are indicated by gray shaded areas of duration  after each spike. It can be seen from this example that different refractory mechanisms give rise to different spiking dynamics.
after each spike. It can be seen from this example that different refractory mechanisms give rise to different spiking dynamics.
 are indicated by a black dot, using one row for each neuron
are indicated by a black dot, using one row for each neuron  , the columns list all
, the columns list all  possible states
possible states  of these
of these  neurons. The tight match between both distributions suggests that the spiking network represents the target probability distribution
neurons. The tight match between both distributions suggests that the spiking network represents the target probability distribution  with high accuracy.
with high accuracy.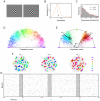
 . (C) Distribution of dominance durations in the trained network under ambiguous input. The red curve shows the Gamma distribution with maximum likelihood on the data. (D) 2-dimensional projection (via population vector) of the distribution
. (C) Distribution of dominance durations in the trained network under ambiguous input. The red curve shows the Gamma distribution with maximum likelihood on the data. (D) 2-dimensional projection (via population vector) of the distribution  encoded in the spiking network showing that it strongly favors coherent global states of arbitrary orientation to incoherent ones (corresponding to population vectors of small magnitude). (E) 2-dimensional projection of the bimodal posterior distribution under an ambiguous input consisting of two different orientations reminiscent of the stimuli shown in A. The black trace shows the temporal evolution of the network state
encoded in the spiking network showing that it strongly favors coherent global states of arbitrary orientation to incoherent ones (corresponding to population vectors of small magnitude). (E) 2-dimensional projection of the bimodal posterior distribution under an ambiguous input consisting of two different orientations reminiscent of the stimuli shown in A. The black trace shows the temporal evolution of the network state  for 500 ms around a perceptual switch. (F) Network states at 3 time points
for 500 ms around a perceptual switch. (F) Network states at 3 time points  marked in E. Neurons that fired in the preceding 20 ms (see gray bar in G) are plotted in the color of their preferred orientation. Inactive neurons are shown in white. While states
marked in E. Neurons that fired in the preceding 20 ms (see gray bar in G) are plotted in the color of their preferred orientation. Inactive neurons are shown in white. While states  and
and  represent rather coherent orientations,
represent rather coherent orientations,  shows an incoherent state corresponding to a perceptual switch. Clamped neurons (which the posterior is condition on) are marked by a black dot. (G) Spike raster of the unclamped neurons during a 500 ms epoch marked by the black trace in E. Gray bars indicate the 20 ms time intervals that define the network states shown in F. Altogether this figure shows that a theoretically rigorous probabilistic inference process can be carried out by a network of spiking neurons with a spike raster that is similar to generic recorded data.
shows an incoherent state corresponding to a perceptual switch. Clamped neurons (which the posterior is condition on) are marked by a black dot. (G) Spike raster of the unclamped neurons during a 500 ms epoch marked by the black trace in E. Gray bars indicate the 20 ms time intervals that define the network states shown in F. Altogether this figure shows that a theoretically rigorous probabilistic inference process can be carried out by a network of spiking neurons with a spike raster that is similar to generic recorded data.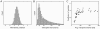
 from the simulation shown in Figure 3 (the membrane potential and spike trace of
from the simulation shown in Figure 3 (the membrane potential and spike trace of  are highlighted in Figure 3). (B) The plot shows the ISI distribution of a typical neuron (again
are highlighted in Figure 3). (B) The plot shows the ISI distribution of a typical neuron (again  from Figure 3) during sampling. The distribution is roughly gamma-shaped, reminiscent of experimentally observed ISI distributions. (C) A scatter plot of the coefficient of variation (CV) versus the average interspike interval (ISI) of each neuron taken from the simulation shown in Figure 3. The value of neuron
from Figure 3) during sampling. The distribution is roughly gamma-shaped, reminiscent of experimentally observed ISI distributions. (C) A scatter plot of the coefficient of variation (CV) versus the average interspike interval (ISI) of each neuron taken from the simulation shown in Figure 3. The value of neuron  from Figure 3 is marked by a cross. The simulated data is in accordance with experimentally observed data.
from Figure 3 is marked by a cross. The simulated data is in accordance with experimentally observed data.
 different Boltzmann distributions over K = 10 variables (with parameters randomly drawn, see setup of Figure 3) and approximations stemming from different neural sampling networks. Networks with absolute refractory mechanism provide the best approximation (as expected from theoretical guarantees). Networks consisting of neurons with relative refractory mechanisms, with only “locally” correct sampling, also provide a close fit to the true distribution (see inset) compared to a fully factorized approximation (assuming correct marginals and independent variables). Furthermore, it can be seen that sampling networks with more realistic, alpha-shaped, additive PSPs still fit the true distribution reasonably well.
different Boltzmann distributions over K = 10 variables (with parameters randomly drawn, see setup of Figure 3) and approximations stemming from different neural sampling networks. Networks with absolute refractory mechanism provide the best approximation (as expected from theoretical guarantees). Networks consisting of neurons with relative refractory mechanisms, with only “locally” correct sampling, also provide a close fit to the true distribution (see inset) compared to a fully factorized approximation (assuming correct marginals and independent variables). Furthermore, it can be seen that sampling networks with more realistic, alpha-shaped, additive PSPs still fit the true distribution reasonably well.
 . The lower panel shows the time course of the refractory function
. The lower panel shows the time course of the refractory function  caused by a single spike of neuron
caused by a single spike of neuron  at
at  . The grey-shaded area of length
. The grey-shaded area of length  indicates the interval of neuron
indicates the interval of neuron  being active (i.e.,
being active (i.e.,  ) due to a single spike of neuron
) due to a single spike of neuron  at time
at time  . (B) Shown is the probability distribution of 5 out of 40 neurons. The plot is similar to Figure 3C, however it is generated with a sampling network that features alpha-shaped, additive PSPs. It can be seen that the network still produces a reasonable approximation to the true Boltzmann distribution (determined by Gibbs sampling).
. (B) Shown is the probability distribution of 5 out of 40 neurons. The plot is similar to Figure 3C, however it is generated with a sampling network that features alpha-shaped, additive PSPs. It can be seen that the network still produces a reasonable approximation to the true Boltzmann distribution (determined by Gibbs sampling).References
-
- Rolls ET, Deco G. Oxford University Press; 2010. The Noisy Brain: Stochastic Dynamics as a Principle of Brain Function. - PubMed
-
- Flight M. Synaptic transmission: On the probability of release. Nat Rev Neurosci. 2010;9:736–737.
-
- GerstnerW, KistlerWM . Cambridge: Cambridge University Press; 2002. Spiking Neuron Models.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

