Stochastic delay accelerates signaling in gene networks
- PMID: 22102802
- PMCID: PMC3213172
- DOI: 10.1371/journal.pcbi.1002264
Stochastic delay accelerates signaling in gene networks
Abstract
The creation of protein from DNA is a dynamic process consisting of numerous reactions, such as transcription, translation and protein folding. Each of these reactions is further comprised of hundreds or thousands of sub-steps that must be completed before a protein is fully mature. Consequently, the time it takes to create a single protein depends on the number of steps in the reaction chain and the nature of each step. One way to account for these reactions in models of gene regulatory networks is to incorporate dynamical delay. However, the stochastic nature of the reactions necessary to produce protein leads to a waiting time that is randomly distributed. Here, we use queueing theory to examine the effects of such distributed delay on the propagation of information through transcriptionally regulated genetic networks. In an analytically tractable model we find that increasing the randomness in protein production delay can increase signaling speed in transcriptional networks. The effect is confirmed in stochastic simulations, and we demonstrate its impact in several common transcriptional motifs. In particular, we show that in feedforward loops signaling time and magnitude are significantly affected by distributed delay. In addition, delay has previously been shown to cause stable oscillations in circuits with negative feedback. We show that the period and the amplitude of the oscillations monotonically decrease as the variability of the delay time increases.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
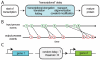
 , and the number of transcription factors needed to overcome the threshold of gene 2,
, and the number of transcription factors needed to overcome the threshold of gene 2,  .
.
 and
and  with equal probability, the mean signaling time decreases with increasing variability in delay time, Eq. (8). Shown are the signaling times (normalized by the time at
with equal probability, the mean signaling time decreases with increasing variability in delay time, Eq. (8). Shown are the signaling times (normalized by the time at  ), versus CV of the delay time for signaling threshold values from
), versus CV of the delay time for signaling threshold values from  (red), through
(red), through  (green) to
(green) to  in steps of 1. Here
in steps of 1. Here  and
and  . When
. When  (brown) increasing randomness in delay time has little effect on the mean. (B) Same as panel (A) but with the probability distribution,
(brown) increasing randomness in delay time has little effect on the mean. (B) Same as panel (A) but with the probability distribution,  , for different values of
, for different values of  . (C) The transition from the small
. (C) The transition from the small  regime to the large
regime to the large  regime occurs when
regime occurs when  . Here we fix
. Here we fix  and between the different curves vary
and between the different curves vary  from
from  (magenta) to
(magenta) to  (orange) in steps of 1. Dashed lines show the asymptotic approximations, Eqs. (9) and (10), which meet at the black line. Panels (D) and (E) are equivalent to panels (A) and (B), with
(orange) in steps of 1. Dashed lines show the asymptotic approximations, Eqs. (9) and (10), which meet at the black line. Panels (D) and (E) are equivalent to panels (A) and (B), with  following a gamma distribution,
following a gamma distribution,  , and
, and  . (F) The coefficient of variation of the signaling time,
. (F) The coefficient of variation of the signaling time,  , as a function of
, as a function of  .
.
 ) and mean delay time (
) and mean delay time ( ). The random time between the initiation of transcription of gene
). The random time between the initiation of transcription of gene  to the full formation of a total of
to the full formation of a total of  proteins
proteins  is denoted
is denoted  , which is an implicit function of
, which is an implicit function of  .
.
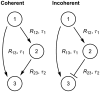
 . (A) Bottom: The expected value of signaling time as a function of the relative standard deviation of the delay time. (B) Top: The shorter pathway is simply the signaling of the first gene to the third. (B) Bottom: Expected signaling time,
. (A) Bottom: The expected value of signaling time as a function of the relative standard deviation of the delay time. (B) Top: The shorter pathway is simply the signaling of the first gene to the third. (B) Bottom: Expected signaling time,  . (C) Top: The output pulse is determined by the amount of time gene
. (C) Top: The output pulse is determined by the amount of time gene  is actively transcribing. This time is simply the difference of the longer path duration (
is actively transcribing. This time is simply the difference of the longer path duration ( ) and the shorter path duration (
) and the shorter path duration ( ). (C) Bottom: Depending on the thresholds
). (C) Bottom: Depending on the thresholds  ,
,  , and
, and  , the expected pulse duration can either increase or decrease as a function of the delay variability. In each of the three plots, the data on the vertical axis are presented relative to the mean pulse duration at
, the expected pulse duration can either increase or decrease as a function of the delay variability. In each of the three plots, the data on the vertical axis are presented relative to the mean pulse duration at  . Here, the colored lines correspond to
. Here, the colored lines correspond to  (blue),
(blue),  (green), and
(green), and  (brown), while
(brown), while  ,
,  . In addition, the protein degradation rates are each
. In addition, the protein degradation rates are each  , all delays are gamma distributed with mean
, all delays are gamma distributed with mean  .
.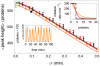
 (orange),
(orange),  (red), and
(red), and  (i.e. step function, black). The top inset shows the shape of the Hill function for the three values of
(i.e. step function, black). The top inset shows the shape of the Hill function for the three values of  , with colors matching those in the main figure. The lower inset shows one realization of the oscillator at parameter values corresponding to the large black circle on the orange (
, with colors matching those in the main figure. The lower inset shows one realization of the oscillator at parameter values corresponding to the large black circle on the orange ( ) curve of the main figure. The average and the standard deviation of the peak heights were calculated from stochastic simulations of
) curve of the main figure. The average and the standard deviation of the peak heights were calculated from stochastic simulations of  oscillations. Here
oscillations. Here  ,
,  ,
,  ,
,  and
and  .
.
 from Example with
from Example with  . The PDFs in red correspond to signal threshold value
. The PDFs in red correspond to signal threshold value  , green to
, green to  and brown to
and brown to  . Here
. Here  and
and  . (B) A 2D view of panel (A) with
. (B) A 2D view of panel (A) with  . Solid lines show analytical results which are nearly indistinguishable from those obtained through stochastic simulation (black lines). Note that the discontinuity in the green curve is due to the discrete nature of the Bernoulli delay distribution. The CDF,
. Solid lines show analytical results which are nearly indistinguishable from those obtained through stochastic simulation (black lines). Note that the discontinuity in the green curve is due to the discrete nature of the Bernoulli delay distribution. The CDF,  , has jump discontinuities that, in light of Eq. (18), produce jump discontinuities in the signaling time PDF. The discontinuity is apparent in both the theoretical prediction (green line) and the stochastic simulations (black line). Panels (C) and (D) are equivalent to panels (A) and (B) with
, has jump discontinuities that, in light of Eq. (18), produce jump discontinuities in the signaling time PDF. The discontinuity is apparent in both the theoretical prediction (green line) and the stochastic simulations (black line). Panels (C) and (D) are equivalent to panels (A) and (B) with  following a gamma distribution. The PDFs were discretized over 200 bins using
following a gamma distribution. The PDFs were discretized over 200 bins using  trials.
trials.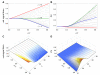
 can increase or decrease as a function of
can increase or decrease as a function of  depending on the value of
depending on the value of  . Here
. Here  . (A)
. (A)  vs. CV of
vs. CV of  for
for  varying from
varying from  (red) to
(red) to  (green) to
(green) to  (blue) using the Bernoulli delay distribution
(blue) using the Bernoulli delay distribution  in Example with
in Example with  . Note the transition that occurs at
. Note the transition that occurs at  . (B) Equivalent to (A), but plotting CV of the signaling time instead of conditional expectation. (C) and (D) Contour plots corresponding to (A) and (B), respectively. Notice that for fixed
. (B) Equivalent to (A), but plotting CV of the signaling time instead of conditional expectation. (C) and (D) Contour plots corresponding to (A) and (B), respectively. Notice that for fixed  , signaling time CV can change non-monotonically with
, signaling time CV can change non-monotonically with  . For instance, at
. For instance, at  , signaling time CV starts low (red), increases to
, signaling time CV starts low (red), increases to  (green) and then decreases thereafter. Plots were obtained through stochastic simulation with
(green) and then decreases thereafter. Plots were obtained through stochastic simulation with  trials.
trials.Similar articles
-
Modeling delay in genetic networks: from delay birth-death processes to delay stochastic differential equations.J Chem Phys. 2014 May 28;140(20):204108. doi: 10.1063/1.4878662. J Chem Phys. 2014. PMID: 24880267 Free PMC article.
-
A simple negative interaction in the positive transcriptional feedback of a single gene is sufficient to produce reliable oscillations.PLoS One. 2011;6(11):e27414. doi: 10.1371/journal.pone.0027414. Epub 2011 Nov 10. PLoS One. 2011. PMID: 22205920 Free PMC article.
-
SGN Sim, a stochastic genetic networks simulator.Bioinformatics. 2007 Mar 15;23(6):777-9. doi: 10.1093/bioinformatics/btm004. Epub 2007 Jan 31. Bioinformatics. 2007. PMID: 17267430
-
Stochastic and delayed stochastic models of gene expression and regulation.Math Biosci. 2010 Jan;223(1):1-11. doi: 10.1016/j.mbs.2009.10.007. Epub 2009 Oct 31. Math Biosci. 2010. PMID: 19883665 Review.
-
Mammalian synthetic biology: engineering of sophisticated gene networks.J Biotechnol. 2007 Jul 15;130(4):329-45. doi: 10.1016/j.jbiotec.2007.05.014. Epub 2007 May 24. J Biotechnol. 2007. PMID: 17602777 Review.
Cited by
-
Simulating ATO Mechanism and EGFR Signaling with Fuzzy Logic and Petri Net.J Biomed Phys Eng. 2021 Jun 1;11(3):325-336. doi: 10.31661/jbpe.v0i0.796. eCollection 2021 Jun. J Biomed Phys Eng. 2021. PMID: 34189121 Free PMC article.
-
The Timing of Transcriptional Regulation in Synthetic Gene Circuits.ACS Synth Biol. 2017 Nov 17;6(11):1996-2002. doi: 10.1021/acssynbio.7b00118. Epub 2017 Sep 5. ACS Synth Biol. 2017. PMID: 28841307 Free PMC article.
-
Density physics-informed neural networks reveal sources of cell heterogeneity in signal transduction.Patterns (N Y). 2023 Dec 26;5(2):100899. doi: 10.1016/j.patter.2023.100899. eCollection 2024 Feb 9. Patterns (N Y). 2023. PMID: 38370126 Free PMC article.
-
Spatially coordinated collective phosphorylation filters spatiotemporal noises for precise circadian timekeeping.iScience. 2023 Apr 1;26(4):106554. doi: 10.1016/j.isci.2023.106554. eCollection 2023 Apr 21. iScience. 2023. PMID: 37123226 Free PMC article.
-
Mechanisms that enhance sustainability of p53 pulses.PLoS One. 2013 Jun 3;8(6):e65242. doi: 10.1371/journal.pone.0065242. Print 2013. PLoS One. 2013. PMID: 23755198 Free PMC article.
References
-
- Jacob F, Monod J. Genetic regulatory mechanisms in synthesis of proteins. J Mol Biol. 1961;3:318–356. - PubMed
-
- Alon U. Network motifs: theory and experimental approaches. Nat Rev Genet. 2007;8:450–461. - PubMed
-
- De Jong H. Modeling and simulation of genetic regulatory systems: a literature review. J Comp Biol. 2002;9:67–103. - PubMed
-
- Kærn M, Blake WJ, Collins JJ. The engineering of gene regulatory networks. Annu Rev Biomed Eng. 2003;5:179–206. - PubMed
-
- Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81:2340–2361.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

