A model of HIV-1 infection with two time delays: mathematical analysis and comparison with patient data

Abstract

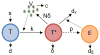
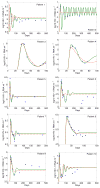
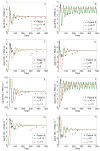
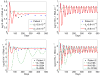
Mathematical models have made considerable contributions to our understanding of HIV dynamics. Introducing time delays to HIV models usually brings challenges to both mathematical analysis of the models and comparison of model predictions with patient data. In this paper, we incorporate two delays, one the time needed for infected cells to produce virions after viral entry and the other the time needed for the adaptive immune response to emerge to control viral replication, into an HIV-1 model. We begin model analysis with proving the positivity and boundedness of the solutions, local stability of the infection-free and infected steady states, and uniform persistence of the system. By developing a few Lyapunov functionals, we obtain conditions ensuring global stability of the steady states. We also fit the model including two delays to viral load data from 10 patients during primary HIV-1 infection and estimate parameter values. Although the delay model provides better fits to patient data (achieving a smaller error between data and modeling prediction) than the one without delays, we could not determine which one is better from the statistical standpoint. This highlights the need of more data sets for model verification and selection when we incorporate time delays into mathematical models to study virus dynamics.

Figure 1

Schematic representation of model (1).

Figure 2

Data fits using the two-delay model (solid curves) and the non-delay model (dashed curves).

Figure 3

The effect of varying immune delay (A–D) or intracellular delay (E–H) on virus dynamics.

Figure 4

The effect of varying killing rate due to immune cells (top panels) or the viral burst size (bottom panels) on virus dynamics.