Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2011 Dec;2(4):377-381.
doi: 10.1016/j.jocs.2011.06.007.

A simple scheme for generating nearly uniform distribution of antipodally symmetric points on the unit sphere

Cheng Guan Koay  1
Affiliations

A simple scheme for generating nearly uniform distribution of antipodally symmetric points on the unit sphere

Cheng Guan Koay. J Comput Sci. 2011 Dec.

Abstract

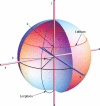
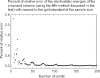
A variant of the Thomson problem, which is about placing a set of points uniformly on the surface of a sphere, is that of generating uniformly distributed points on the sphere that are endowed with antipodal symmetry, i.e., if x is an element of the point set then -x is also an element of that point set. Point sets with antipodal symmetry are of special importance to many scientific and engineering applications. Although this type of point sets may be generated through the minimization of a slightly modified electrostatic potential, the optimization procedure becomes unwieldy when the size of the point set increases beyond a few thousands. Therefore, it is desirable to have a deterministic scheme capable of generating this type of point set with near uniformity. In this work, we will present a simple deterministic scheme to generate nearly uniform point sets with antipodal symmetry.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Latitude and longitude on the unit sphere.
Figure 2
Figure 2
The number of latitude lines, n, as a function of the number of points, K. The red line is the asymptotic solution of n and the discontinuous blue line is the iterative solution of n rounded to the nearest integer.
Figure 3
Figure 3
Antipodally symmetric point sets with (A) 100 and (B) 800 points on the upper hemisphere or respectively 200 and 1600 points on the whole sphere.
Figure 4
Figure 4
Percent of relative error of the proposed scheme compared to that of the gold standard.
See this image and copyright information in PMC

References

    1. Ahmad R, Deng Y, Vikram DS, Clymer B, Srinivasan P, Zweier JL, Kuppusamy P. Quasi Monte Carlo-based isotropic distribution of gradient directions for improved reconstruction quality of 3D EPR imaging. Journal of Magnetic Resonance. 2007;184(2):236–245. - PMC - PubMed
    1. Anderson AW. Measurement of fiber orientation distributions using high angular resolution diffusion imaging. Magnetic Resonance in Medicine. 2005;54(5):1195–1206. - PubMed
    1. Basser PJ, Mattiello J, Le Bihan D. MR diffusion tensor spectroscopy and imaging. Biophys. J. 1994;66(1):259–267. - PMC - PubMed
    1. Bauer R. Distribution of points on a sphere with application to star catalogs. Journal of guidance control and dynamic. 2000;23:130–137.
    1. Deriche R, Calder J, Descoteaux M. Optimal real-time Q-ball imaging using regularized Kalman filtering with incremental orientation sets. Medical Image Analysis. 2009;13(4):564–579. - PubMed

LinkOut - more resources