Eco-evolutionary feedback and the invasion of cooperation in prisoner's dilemma games

Abstract

Unveiling the origin and forms of cooperation in nature poses profound challenges in evolutionary ecology. The prisoner's dilemma game is an important metaphor for studying the evolution of cooperation. We here classified potential mechanisms for cooperation evolution into schemes of frequency- and density-dependent selection, and focused on the density-dependent selection in the ecological prisoner's dilemma games. We found that, although assortative encounter is still the necessary condition in ecological games for cooperation evolution, a harsh environment, indicated by a high mortality, can foster the invasion of cooperation. The Hamilton rule provides a fundamental condition for the evolution of cooperation by ensuring an enhanced relatedness between players in low-density populations. Incorporating ecological dynamics into evolutionary games opens up a much wider window for the evolution of cooperation, and exhibits a variety of complex behaviors of dynamics, such as limit and heteroclinic cycles. An alternative evolutionary, or rather succession, sequence was proposed that cooperation first appears in harsh environments, followed by the invasion of defection, which leads to a common catastrophe. The rise of cooperation (and altruism), thus, could be much easier in the density-dependent ecological games than in the classic frequency-dependent evolutionary games.

Figure 1. The dependence of dynamical behaviors on model parameters.

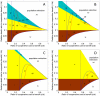
Brown part and part iv, , have two boundary equilibriums: one for cooperators; the other for defectors. Yellow part, , has only one boundary equilibrium for cooperators. Cyan part, , has two boundary equilibriums both for cooperators. The area encircled by blue curves indicates the existence of interior equilibrium of cooperation-defect coexistence. The three red lines on (A) and (B), from bottom to top, indicate the node-focus bifurcation, Hopf bifurcation and the heteroclinic bifurcation, respectively, and the red lines on (C) and (D) indicate the node-focus bifurcation. Area on the left side of the vertical dotted line indicates the invasion condition for cooperation in the frequency-dependent selection (i.e. ). Parameters are and m = 0.1, 0.2, 0.3 and 0.55, respectively, for panel (A) to (D).

Figure 2. The behaviors of the dynamics of ecological prisoner's dilemma games on a phase plane.

Plots (i)–(xv) correspond to part i–xv in Fig. 1, respectively. Solid circles represent stable equilibriums; open circles represent unstable equilibriums. Parameters are , , for all diagrams, except and for (i), and for (ii), and for (iii), and for (iv), and for (v), and for (vi), and for (vii), and for (viii), and for (ix), and for (x), and for (xi), and for (xii), and for (xiii), and for (xiv), and and for (xv).

Figure 3. Spatial patterns of the ecological PDG on a 401×401 lattice.

The color brightness indicates the probabilities that each site is occupied by a cooperator (red) or a defector (green), or remains empty (black) (as in Wakano et al. 2009). Initially, the central site is occupied by a cooperator with a probability of 0.1 or by a defector with the same probability, and the other sites are completely empty. Parameters are the same as Fig. 2 viii as for the dynamics of periodic oscillation. First snapshot is taken at time 1500; the others start from time 4500, with a temporal interval of 1500 time steps. See Animation S2 and Appendix S3 for details.