Higher-order interactions characterized in cortical activity
- PMID: 22131413
- PMCID: PMC6623824
- DOI: 10.1523/JNEUROSCI.3127-11.2011
Higher-order interactions characterized in cortical activity
Abstract
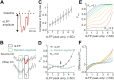
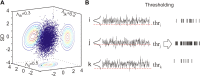
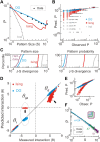
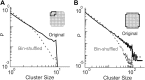
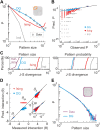
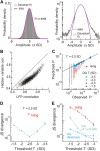
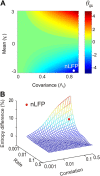
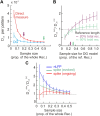
In the cortex, the interactions among neurons give rise to transient coherent activity patterns that underlie perception, cognition, and action. Recently, it was actively debated whether the most basic interactions, i.e., the pairwise correlations between neurons or groups of neurons, suffice to explain those observed activity patterns. So far, the evidence reported is controversial. Importantly, the overall organization of neuronal interactions and the mechanisms underlying their generation, especially those of high-order interactions, have remained elusive. Here we show that higher-order interactions are required to properly account for cortical dynamics such as ongoing neuronal avalanches in the alert monkey and evoked visual responses in the anesthetized cat. A Gaussian interaction model that utilizes the observed pairwise correlations and event rates and that applies intrinsic thresholding identifies those higher-order interactions correctly, both in cortical local field potentials and spiking activities. This allows for accurate prediction of large neuronal population activities as required, e.g., in brain-machine interface paradigms. Our results demonstrate that higher-order interactions are inherent properties of cortical dynamics and suggest a simple solution to overcome the apparent formidable complexity previously thought to be intrinsic to those interactions.
Figures




References
-
- Abeles M, Bergman H, Margalit E, Vaadia E. Spatiotemporal firing patterns in the frontal cortex of behaving monkeys. J Neurophysiol. 1993;70:1629–1638. - PubMed
-
- Amari S. Information geometry on hierarchy of probability distributions. IEEE Trans Inform Theory. 2001;47:1701–1711.
-
- Amari S, Nakahara H, Wu S, Sakai Y. Synchronous firing and higher-order interactions in neuron pool. Neural Comput. 2003;15:127–142. - PubMed
-
- Baum EB. What is thought? Cambridge: MA MIT; 2004. Chap 6.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
