Shapes of discoid intracellular compartments with small relative volumes

Abstract

A prominent feature of many intracellular compartments is a large membrane surface area relative to their luminal volume, i.e., the small relative volume. In this study we present a theoretical analysis of discoid membrane compartments with a small relative volume and then compare the theoretical results to quantitative morphological assessment of fusiform vesicles in urinary bladder umbrella cells. Specifically, we employ three established extensions of the standard approach to lipid membrane shape calculation and determine the shapes that could be expected according to three scenarios of membrane shaping: membrane adhesion in the central discoid part, curvature driven lateral segregation of membrane constituents, and existence of stiffer membrane regions, e.g., support by protein scaffolds. The main characteristics of each scenario are analyzed. The results indicate that even though all three scenarios can lead to similar shapes, there are values of model parameters that yield qualitatively distinctive shapes. Consequently, a distinctive shape of an intracellular compartment may reveal its membrane shaping mechanism and the membrane structure. The observed shapes of fusiform vesicles fall into two qualitatively different classes, yet they are all consistent with the theoretical results and the current understanding of their structure and function.

Figure 1. Schematic representation of three scenarios of membrane shaping.

A) The discoid shape can be stabilized by adhesion between the membranes in the central part, possibly mediated by interacting luminal domains of transmembrane proteins (red). B) Weak lateral segregation of mobile membrane constituents, e.g., lipids, proteins or membrane microdomains. Segregation of wedge-shaped constituents (blue) into the rim and cylindrical constituents (red) into the flat membrane parts relaxes the bending stress in the membrane. Within the weak lateral segregation scenario, the membrane material properties vary continuously across the membrane and no distinct membrane regions with defined boundaries are observed. C) Formation of stiffer membrane regions with a defined spontaneous curvature and defined boundaries, e.g., formation of protein scaffolds that support the membrane (red). The central discoid part can be supported by a scaffold with a small spontaneous curvature (top) and the discoid rims can be supported by a highly curved scaffold (bottom).

Figure 2. EM micrographs of fusiform vesicles in urothelial umbrella cells.

A) Apical region of an umbrella cell with numerous FVs with small relative volumes. Apical plasma membrane of the cells is composed of urothelial plaques (big arrows) and hinge regions (small arrows). In B–E, the plaque regions of analyzed FVs are highlighted by light red lines, and the hinge regions by light blue lines. The relative volumes of FVs are approximately 0.1 (B–D) and 0.3 (E). The relative sizes of plaque regions with respect to the total FV surface area are: 50% (B), 63% (C), 88% (D), and 58% (E). Bars: 1 m (A), 100 nm (B–E).

Figure 3. Shape features of discoid compartments with homogeneous membrane.

A) Shape transformations due to a decreasing relative volume at a vanishing relative difference between the lateral tensions of the bilayer leaflets (). At , the shape is the well-known biconcave shape of a red blood cell (shape a). Decreasing the volume leads to a contact of the membrane at the discoid center (shape b, ) and then to an increase of the contact surface area (shape c, ). B) Phase diagram describing the values of and at which the membrane of a discoid compartment comes into contact with itself. The positions of the shapes a, b and c are presented.

Figure 4. Shape changes due to adhesion in the central discoid part (top, shapes d and e) and lateral segregation of membrane constituents (bottom, shapes f and g).

Shape c is the shape from the standard homogeneous model (Fig. 3A). The adhesion strength is represented by the relative adhesion constant ; an increase of increases the contact surface area. The impact of the lateral segregation is described by parameter ; an increase in corresponds to more convex shapes with a smaller contact surface area. The relative volume of all shapes is 0.1.

Figure 5. Examples of shapes with two distinct membrane regions.

The stiffer membrane regions are presented by thick red lines and the soft membrane regions by thin black lines. The relative stiffness (), the spontaneous curvature () and the relative size of the stiffer regions, and the relative volume of the compartment () are denoted. The spontaneous curvature of the soft region is zero. A) Effects of an increasing size of a very stiff region with in the central discoid part. B) Effects of an increasing size of a curved () stiffer region supporting the discoid rim. C) Effects of an increasing relative volume in the case corresponding to the observed FV: the stiffer region is in the central discoid part, it occupies 60% of the total membrane surface area and has . The relative stiffness of the stiffer region is chosen to be 40.

Figure 6. Phase diagrams showing the regions where the compartment's membrane is not in self-contact (dashed regions).

The calculated dependence on the relative stiffness and the relative size of the stiffer membrane region is presented. The diagrams correspond to the shapes presented in Fig. 5 A and B. A) The stiffer membrane region has zero spontaneous curvature and supports the central discoid parts, shapes h through m in Fig. 5A. B) The stiffer region is c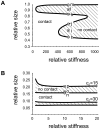urved and supports the discoid rim, shapes n through p in Fig. 5B. The diagram is given for two values of the spontaneous curvature in the rim ( and ). The crossed circles correspond to the shapes presented in Fig. 5.