A Partial Least Squares based algorithm for parsimonious variable selection

Abstract

Background: In genomics, a commonly encountered problem is to extract a subset of variables out of a large set of explanatory variables associated with one or several quantitative or qualitative response variables. An example is to identify associations between codon-usage and phylogeny based definitions of taxonomic groups at different taxonomic levels. Maximum understandability with the smallest number of selected variables, consistency of the selected variables, as well as variation of model performance on test data, are issues to be addressed for such problems.

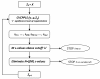
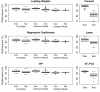
Results: We present an algorithm balancing the parsimony and the predictive performance of a model. The algorithm is based on variable selection using reduced-rank Partial Least Squares with a regularized elimination. Allowing a marginal decrease in model performance results in a substantial decrease in the number of selected variables. This significantly improves the understandability of the model. Within the approach we have tested and compared three different criteria commonly used in the Partial Least Square modeling paradigm for variable selection; loading weights, regression coefficients and variable importance on projections. The algorithm is applied to a problem of identifying codon variations discriminating different bacterial taxa, which is of particular interest in classifying metagenomics samples. The results are compared with a classical forward selection algorithm, the much used Lasso algorithm as well as Soft-threshold Partial Least Squares variable selection.

Conclusions: A regularized elimination algorithm based on Partial Least Squares produces results that increase understandability and consistency and reduces the classification error on test data compared to standard approaches.

Figure 1

Flow chart. The flow chart illustrates the proposed algorithm for variable selection.

Figure 2

An overview of the testing/training. An overview of the testing/training procedure used in this study. The rectangles illustrate the predictor matrix. At level 1 we split the data into a test set and training set (25/75) to be used by all four methods listed on the right. This was repeated 100 times. Inside our suggested method, the stepwise elimination, there are two levels of cross-validation. First a 10-fold cross-validation was used to optimize selection parameters f and d, and at level 3 leave-one-out cross-validation was used to optimize the regularized CPPLS method.

Figure 3

A typical elimination. A typical elimination is shown based on the data for phylum Actinobacteria. Each dot in the figure indicates one iteration. The procedure starts on the left hand side, with the full model. After some iterations performance(P), which reflects the percentage of correctly classified samples, has increased, and reaches a maximum. Further elimination reduces performance, but only marginally. When elimination becomes too severe, the performance drops substantially. Finally, the selected model is found where we have the smallest model with performance not significantly worse than the maximum.

Figure 4

The distribution of selected variables. The distribution of the number of variables selected by the optimum model and selected model for loading weights, VIP and regression coefficients is presented in upper panels, while lower panels display similar for Forward, Lasso and ST-PLS. The horizontal axes are the number of retained variables as percentage of the full model (with 4160 variables). All results are based on 100 random samples from the full data set, where 75% of the objects are used as training data and 25% as test data in each sample.

Figure 5

Performance comparison. The left panel presents the distribution of performance of in the full model, optimum model and selected models on test and training data sets for loading weights, VIP and regression coefficients, while the right panels display similar for Forward, Lasso and ST-PLS. All results are based on 100 random samples from the full data set, where 75% of the objects are used as training data and 25% as test data in each sample.

Figure 6

Selectivity score. The selectivity score is sorted in descending order for each criterion loading weights, regression coefficients significance and VIP in the left panels, while right panels display similar for Forward, Lasso and ST-PLS. Only the first 500 values (out of 4160) are shown.