Heterozygote advantage as a natural consequence of adaptation in diploids
- PMID: 22143780
- PMCID: PMC3251125
- DOI: 10.1073/pnas.1114573108
Heterozygote advantage as a natural consequence of adaptation in diploids
Abstract
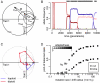
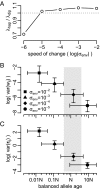
Molecular adaptation is typically assumed to proceed by sequential fixation of beneficial mutations. In diploids, this picture presupposes that for most adaptive mutations, the homozygotes have a higher fitness than the heterozygotes. Here, we show that contrary to this expectation, a substantial proportion of adaptive mutations should display heterozygote advantage. This feature of adaptation in diploids emerges naturally from the primary importance of the fitness of heterozygotes for the invasion of new adaptive mutations. We formalize this result in the framework of Fisher's influential geometric model of adaptation. We find that in diploids, adaptation should often proceed through a succession of short-lived balanced states that maintain substantially higher levels of phenotypic and fitness variation in the population compared with classic adaptive walks. In fast-changing environments, this variation produces a diversity advantage that allows diploids to remain better adapted compared with haploids despite the disadvantage associated with the presence of unfit homozygotes. The short-lived balanced states arising during adaptive walks should be mostly invisible to current scans for long-term balancing selection. Instead, they should leave signatures of incomplete selective sweeps, which do appear to be common in many species. Our results also raise the possibility that balancing selection, as a natural consequence of frequent adaptation, might play a more prominent role among the forces maintaining genetic variation than is commonly recognized.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

References
-
- Haldane JBS. A mathematical theory of natural and artificial selection, part V: Selection and mutation. Math Proc Camb Philos Soc. 1927;23:838–844.
-
- Carroll SB. Evo-devo and an expanding evolutionary synthesis: A genetic theory of morphological evolution. Cell. 2008;134(1):25–36. - PubMed
-
- Lemos B, Meiklejohn CD, Caceres M, Hartl DL. Rates of divergence in gene expression profiles of primates, mice, and flies: Stabilizing selection and variability among functional categories. Evolution. 2005;59:126–137. - PubMed
-
- Denver DR, et al. The transcriptional consequences of mutation and natural selection in Caenorhabditis elegans. Nat Genet. 2005;37:544–548. - PubMed
-
- Rifkin SA, Houle D, Kim J, White KP. A mutation accumulation assay reveals a broad capacity for rapid evolution of gene expression. Nature. 2005;438:220–223. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

