Population divergence with or without admixture: selecting models using an ABC approach
- PMID: 22146980
- PMCID: PMC3330690
- DOI: 10.1038/hdy.2011.116
Population divergence with or without admixture: selecting models using an ABC approach
Abstract
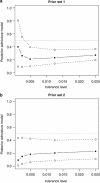
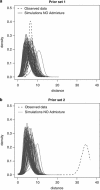
Genetic data have been widely used to reconstruct the demographic history of populations, including the estimation of migration rates, divergence times and relative admixture contribution from different populations. Recently, increasing interest has been given to the ability of genetic data to distinguish alternative models. One of the issues that has plagued this kind of inference is that ancestral shared polymorphism is often difficult to separate from admixture or gene flow. Here, we applied an approximate Bayesian computation (ABC) approach to select the model that best fits microsatellite data among alternative splitting and admixture models. We performed a simulation study and showed that with reasonably large data sets (20 loci) it is possible to identify with a high level of accuracy the model that generated the data. This suggests that it is possible to distinguish genetic patterns due to past admixture events from those due to shared polymorphism (population split without admixture). We then apply this approach to microsatellite data from an endangered and endemic Iberian freshwater fish species, in which a clustering analysis suggested that one of the populations could be admixed. In contrast, our results suggest that the observed genetic patterns are better explained by a population split model without admixture.
Figures
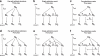



Similar articles
-
Complex genetic admixture histories reconstructed with Approximate Bayesian Computation.Mol Ecol Resour. 2021 May;21(4):1098-1117. doi: 10.1111/1755-0998.13325. Epub 2021 Feb 26. Mol Ecol Resour. 2021. PMID: 33452723 Free PMC article.
-
The population demography of Betula maximowicziana, a cool-temperate tree species in Japan, in relation to the last glacial period: its admixture-like genetic structure is the result of simple population splitting not admixing.Mol Ecol. 2015 Apr;24(7):1403-18. doi: 10.1111/mec.13123. Epub 2015 Mar 23. Mol Ecol. 2015. PMID: 25706115
-
Approximate Bayesian computation for modular inference problems with many parameters: the example of migration rates.Mol Ecol. 2013 Feb;22(4):987-1002. doi: 10.1111/mec.12165. Epub 2013 Jan 10. Mol Ecol. 2013. PMID: 23301635
-
On the use of kernel approximate Bayesian computation to infer population history.Genes Genet Syst. 2015;90(3):153-62. doi: 10.1266/ggs.90.153. Genes Genet Syst. 2015. PMID: 26510570 Review.
-
Human genetic admixture through the lens of population genomics.Philos Trans R Soc Lond B Biol Sci. 2022 Jun 6;377(1852):20200410. doi: 10.1098/rstb.2020.0410. Epub 2022 Apr 18. Philos Trans R Soc Lond B Biol Sci. 2022. PMID: 35430881 Free PMC article. Review.
Cited by
-
Approximate Bayesian computational methods to estimate the strength of divergent selection in population genomics models.J Comput Math Data Sci. 2024 Mar;10:100091. doi: 10.1016/j.jcmds.2024.100091. Epub 2024 Feb 7. J Comput Math Data Sci. 2024. PMID: 38616846 Free PMC article.
-
History of the fragmentation of the African rain forest in the Dahomey Gap: insight from the demographic history of Terminalia superba.Heredity (Edinb). 2018 Jun;120(6):547-561. doi: 10.1038/s41437-017-0035-0. Epub 2017 Dec 27. Heredity (Edinb). 2018. PMID: 29279603 Free PMC article.
-
Informing conservation strategies with museum genomics: Long-term effects of past anthropogenic persecution on the elusive European wildcat.Ecol Evol. 2021 Dec 3;11(24):17932-17951. doi: 10.1002/ece3.8385. eCollection 2021 Dec. Ecol Evol. 2021. PMID: 35003648 Free PMC article.
-
Using ABC and microsatellite data to detect multiple introductions of invasive species from a single source.Heredity (Edinb). 2015 Sep;115(3):262-72. doi: 10.1038/hdy.2015.38. Epub 2015 Apr 29. Heredity (Edinb). 2015. PMID: 25920671 Free PMC article.
-
The population history of Garra orientalis (Teleostei: Cyprinidae) using mitochondrial DNA and microsatellite data with approximate Bayesian computation.BMC Evol Biol. 2016 Apr 11;16:73. doi: 10.1186/s12862-016-0645-9. BMC Evol Biol. 2016. PMID: 27068356 Free PMC article.
References
-
- Alves MJ, Coelho MM. Genetic variation and population subdivision of the endangered Iberian cyprinid Chondrostoma lusitanicum. J Fish Biol. 1994;44:627–636.
-
- Beaumont M. Approximate Bayesian computation in evolution and ecology. Annu Rev Ecol Evol Syst. 2010;41:379–406.
-
- Beaumont MA.2008. Joint determination of tree topology and population history. In: Matsumura S, Forster P, Renfrew C (eds) Simulation, Genetics, and Human Prehistory. McDonald Institute for Archaeological Research: Cambridge; 135–154.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

