Protein 3D structure computed from evolutionary sequence variation
- PMID: 22163331
- PMCID: PMC3233603
- DOI: 10.1371/journal.pone.0028766
Protein 3D structure computed from evolutionary sequence variation
Abstract
The evolutionary trajectory of a protein through sequence space is constrained by its function. Collections of sequence homologs record the outcomes of millions of evolutionary experiments in which the protein evolves according to these constraints. Deciphering the evolutionary record held in these sequences and exploiting it for predictive and engineering purposes presents a formidable challenge. The potential benefit of solving this challenge is amplified by the advent of inexpensive high-throughput genomic sequencing.In this paper we ask whether we can infer evolutionary constraints from a set of sequence homologs of a protein. The challenge is to distinguish true co-evolution couplings from the noisy set of observed correlations. We address this challenge using a maximum entropy model of the protein sequence, constrained by the statistics of the multiple sequence alignment, to infer residue pair couplings. Surprisingly, we find that the strength of these inferred couplings is an excellent predictor of residue-residue proximity in folded structures. Indeed, the top-scoring residue couplings are sufficiently accurate and well-distributed to define the 3D protein fold with remarkable accuracy.We quantify this observation by computing, from sequence alone, all-atom 3D structures of fifteen test proteins from different fold classes, ranging in size from 50 to 260 residues, including a G-protein coupled receptor. These blinded inferences are de novo, i.e., they do not use homology modeling or sequence-similar fragments from known structures. The co-evolution signals provide sufficient information to determine accurate 3D protein structure to 2.7-4.8 Å C(α)-RMSD error relative to the observed structure, over at least two-thirds of the protein (method called EVfold, details at http://EVfold.org). This discovery provides insight into essential interactions constraining protein evolution and will facilitate a comprehensive survey of the universe of protein structures, new strategies in protein and drug design, and the identification of functional genetic variants in normal and disease genomes.
Conflict of interest statement
Figures

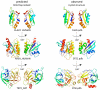
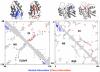



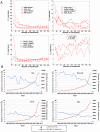

References
-
- Altschuh D, Lesk AM, Bloomer AC, Klug A. Correlation of co-ordinated amino acid substitutions with function in viruses related to tobacco mosaic virus. J Mol Biol. 1987;193:693–707. - PubMed
-
- Altschuh D, Vernet T, Berti P, Moras D, Nagai K. Coordinated amino acid changes in homologous protein families. Protein Eng. 1988;2:193–199. - PubMed
-
- Göbel U, Sander C, Schneider R, Valencia A. Correlated mutations and residue contacts in proteins. Proteins. 1994;18:309–317. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

