The role of exploratory conditions in bio-inspired tactile sensing of single topogical features
- PMID: 22164054
- PMCID: PMC3231713
- DOI: 10.3390/s110807934
The role of exploratory conditions in bio-inspired tactile sensing of single topogical features
Abstract
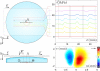
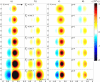
We investigate the mechanism of tactile transduction during active exploration of finely textured surfaces using a tactile sensor mimicking the human fingertip. We focus in particular on the role of exploratory conditions in shaping the subcutaneous mechanical signals. The sensor has been designed by integrating a linear array of MEMS micro-force sensors in an elastomer layer. We measure the response of the sensors to the passage of elementary topographical features at constant velocity and normal load, such as a small hole on a flat substrate. Each sensor's response is found to strongly depend on its relative location with respect to the substrate/skin contact zone, a result which can be quantitatively understood within the scope of a linear model of tactile transduction. The modification of the response induced by varying other parameters, such as the thickness of the elastic layer and the confining load, are also correctly captured by this model. We further demonstrate that the knowledge of these characteristic responses allows one to dynamically evaluate the position of a small hole within the contact zone, based on the micro-force sensors signals, with a spatial resolution an order of magnitude better than the intrinsic resolution of individual sensors. Consequences of these observations on robotic tactile sensing are briefly discussed.
Keywords: MEMS tactile sensor array; biomimetic sensor; friction; human tactile perception; hyperacuity; mechanoreceptors; receptive field; topological feature localization.
Figures
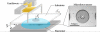


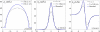



References
-
- Hollins M. Somesthetic senses. Annu. Rev. Psychol. 2010;61:243–271. - PubMed
-
- Johansson R, Flanagan J. Coding and use of tactile signals from the fingertips in object manipulation tasks. Nat. Rev. Neurosci. 2009;10:345–59. - PubMed
-
- Westling G, Johannson RS. Factors influencing the force control during precision grip. Exp. Brain Res. 1984;53:277–284. - PubMed
-
- Dahiya RS, Metta G, Valle M, Sandini G. Tactile sensing—From humans to humanoids. IEEE Trans. Rob. 2010;26:1–20.
-
- Maheshwari V, Saraf RF. High-resolution thin-film device to sense texture by touch. Science. 2006;312:1501–1504. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

