Analytical modeling for the bending resonant frequency of multilayered microresonators with variable cross-section

Abstract

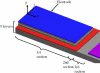
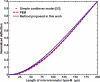
Multilayered microresonators commonly use sensitive coating or piezoelectric layers for detection of mass and gas. Most of these microresonators have a variable cross-section that complicates the prediction of their fundamental resonant frequency (generally of the bending mode) through conventional analytical models. In this paper, we present an analytical model to estimate the first resonant frequency and deflection curve of single-clamped multilayered microresonators with variable cross-section. The analytical model is obtained using the Rayleigh and Macaulay methods, as well as the Euler-Bernoulli beam theory. Our model is applied to two multilayered microresonators with piezoelectric excitation reported in the literature. Both microresonators are composed by layers of seven different materials. The results of our analytical model agree very well with those obtained from finite element models (FEMs) and experimental data. Our analytical model can be used to determine the suitable dimensions of the microresonator's layers in order to obtain a microresonator that operates at a resonant frequency necessary for a particular application.

Keywords: Euler-Bernoulli beam theory; Macaulay method; Rayleigh’s method; bending resonant frequency; multilayered microresonator.

Figure 1.

View of the multilayered microresonator with variable cross section proposed in this work.

Figure 2.

Geometrical nomenclature proposed for the kth layer located on the jth section of the proposed multilayered microresonator.

Figure 3.

Examples of multilayered microresonators obtained from the proposed multilayered microresonator. These microresonators could are composed by silicon layers with (a–b) sensitive coating and (c–d) piezoelectric layers.

Figure 4.

View of the load types acting on the proposed multilayered microresonator.

Figure 5.

SEM micrograph of the multilayered microresonator type-A [46]. Reprinted with permission from Elsevier Science B.V. Copyright© 2009.

Figure 6.

SEM micrograph of the multilayered microresonator type-B [47]. Reprinted with permission from Japan Society of Applied Physics. Copyright© 2007.

Figure 7.

Geometrical configuration of the layers and load types on the microresonator type-A. This figure is not drawn in scale.

Figure 8.

Detail view of the layers located on the first three sections of the microresonator type-A. This figure is not drawn in scale.

Figure 9.

Detail view of the layers located on the first three sections of the microresonator type-A. This figure is not drawn in scale.

Figure 10.

Geometrical configuration of the layers and load types on the microresonator type-B. This figure is not drawn in scale.

Figure 11.

Detail view of the layers located on the first three sections of the microresonator type-B. This figure is not drawn in scale.

Figure 12.

First bending mode of the microresonator type-A obtained using a FEM.

Figure 13.

First bending mode of the microresonator type-B obtained using a FEM.

Figure 14.

Normalized deflection y(x)/y_max of the microresonator type-A obtained through our analytical model, a FEM, and a simple cantilever model.

Figure 15.

Normalized deflection y(x)/y_max of the microresonator type-B obtained through our analytical model, a FEM, and a simple cantilever model.