The dichotomy in degree correlation of biological networks

Abstract

Most complex networks from different areas such as biology, sociology or technology, show a correlation on node degree where the possibility of a link between two nodes depends on their connectivity. It is widely believed that complex networks are either disassortative (links between hubs are systematically suppressed) or assortative (links between hubs are enhanced). In this paper, we analyze a variety of biological networks and find that they generally show a dichotomous degree correlation. We find that many properties of biological networks can be explained by this dichotomy in degree correlation, including the neighborhood connectivity, the sickle-shaped clustering coefficient distribution and the modularity structure. This dichotomy distinguishes biological networks from real disassortative networks or assortative networks such as the Internet and social networks. We suggest that the modular structure of networks accounts for the dichotomy in degree correlation and vice versa, shedding light on the source of modularity in biological networks. We further show that a robust and well connected network necessitates the dichotomy of degree correlation, suggestive of an evolutionary motivation for its existence. Finally, we suggest that a dichotomous degree correlation favors a centrally connected modular network, by which the integrity of network and specificity of modules might be reconciled.

Figure 1. Disassortative and assortative networks.

Schematic illustration of a disassortative network (A) and an assortative network (B). C. The 15 best connected proteins and their direct links to other proteins of yeast protein network constructed by proteins localized in nucleus. D. The rest of network after removal of the 15 best connected nodes. Nodes disconnected to the largest component are not shown. A predominant feature of B and D is the over-abundance of links between low connected nodes.

Figure 2. Correlation profiles of complex networks.

A. The plot of Z-score of Internet at AS level which is known to be disassortative, where the red color reflects the affinity of nodes and blue color reflects the repulsion between nodes. B. The profile of a social network constructed by collaborations between authors who co-authored a paper, which is known to be assortative. C. The correlation profile of yeast PIN constructed by HC dataset. D. The correlation profile of yeast GIN. E. The profile of yeast metabolic network abstracted from KEGG. F. The correlation profile of HC dataset after removing interactions between proteins within the same complex. Note that through C to F, at least 99% nodes of biological networks are localized in the lower left corner where the diagonal is colored red.

Figure 3. Correlations between node connectivity and its neighborhood connectivity.

A. The nearest neighbors' average connectivity K_nc, of nodes with connectivity k for Internet at AS level, and for the rest of network with top 1% best connected nodes removed (solid triangle). B. The same as A but for social network of co-authored relationship. C. Correlations of biological networks: PIN of HC dataset (red), GIN (green) and yeast metabolic network (blue). D. Correlations of biological networks after removing top ∼1% best connected nodes (detailed numbers of hubs removed are shown in Table 1). 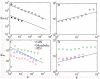The solid lines in A and C correspond to ; the solid lines in B and D correspond to . Note that the solid lines in C and D are not fitted to biological networks; they are drawn to compare with Internet and social network.

Figure 4. The dichotomy of degree correlation and its reflection on clustering coefficient distribution.

The clustering coefficient distribution of Internet at AS level (A) and social network of co-authored relationship (B). C. The sickle-shaped C(k) curve of biological networks: PIN of HC dataset (red), GIN (green) and yeast metabolic network (blue). The inset displays the C(k) curves of 100 random dichotomized networks (each containing 10,000 nodes with P(k)∼k ^−2.4, of which links of the top 0.5% best connected nodes are disassortative while those of other nodes are assortative). D. The assortative coefficient curves r(k) for the three biological networks. In A, C and D, the solid lines correspond to C(k)∼k ⁻¹, which are drawn to compare with the hierarchical model.

Figure 5. Degree correlation and modularity.

A. The correlation profile of the triangle-favoring network. Note that the network is assortative. B. The correlation profile of the anti-correlation favoring network. Note that the network is disassortative. C. The correlation profile of the composite network, which presents a dichotomy in degree correlation. D. The two C(k) curves of the composite network (T = 1, black circles) and PIN of HC dataset (red circles) overlaps in a great extent. E. The strength of modularity, M and the relative size of largest component, S during the removal of a fraction f _e of intermodular edges for the triangle-favoring (TF) network, the anti-correlation favoring (ACF) network, the composite network and PIN of HC dataset.

Figure 6. Robustness and interconnectivity of the network under targeted attacks.

A. Comparison of the size of the largest component between disassortative, assortative and dichotomized network models, each containing 10,000 nodes with P(k)∼k ^−2.4. B. Comparison of network diameter as a function of the fraction f of removed best connected nodes. Note that the size of the largest component of unperturbed dichotomized network (f = 0) is larger than that of assortative network, while the diameter is smaller than it, indicating that the dichotomy of degree correlation generates a more interconnected web. C. The size of the largest component in function of f, between PIN of HC dataset and a random network with similar level of anti-correlation (generated by rewiring links of PIN and by setting the parameter p = 0.05, see materials and methods). D. The same as C but between GIN and a random network with similar level of anti-correlation (generated by setting the parameter p = 0.1).

Figure 7. Schematic models of disassortative, dichotomized and assortative networks.

A. Schematic model of a disassortative network (inset) and a random network under the principle of the model. B. The same as A but for dichotomized network. C. The same as A but for assortative network. Each of the random networks has the same number of nodes (100), the same number of edges (94) and the same degree distribution. Disassortative network model in A suggests a modular structure with modules separately distributed and pair-wisely connected, whereas C suggests a highly integrated network with nodes integrated by a core of fully connected hubs. The dichotomized network in B suggests a centrally connected modular structure where modules are tightly connected to each other rather than dispersedly distributed.

Figure 8. Dichotomous modules.

A. Modules organized around YLR423C YBR160W. Assortative links are colored red and disassortative links are colored blue. B. Modules organized around YBR160W. C. Two modules organized around YDL239C and YML264C are connected to each other through assortative links. D. Assortative hubs are more essential than disassortative hubs (chi-square test).