Quantifying density fluctuations in volumes of all shapes and sizes using indirect umbrella sampling
- PMID: 22184480
- PMCID: PMC3241221
- DOI: 10.1007/s10955-011-0269-9
Quantifying density fluctuations in volumes of all shapes and sizes using indirect umbrella sampling
Abstract
Water density fluctuations are an important statistical mechanical observable that is related to many-body correlations, as well as hydrophobic hydration and interactions. Local water density fluctuations at a solid-water surface have also been proposed as a measure of it's hydrophobicity. These fluctuations can be quantified by calculating the probability, P(v)(N), of observing N waters in a probe volume of interest v. When v is large, calculating P(v)(N) using molecular dynamics simulations is challenging, as the probability of observing very few waters is exponentially small, and the standard procedure for overcoming this problem (umbrella sampling in N) leads to undesirable impulsive forces. Patel et al. [J. Phys. Chem. B, 114, 1632 (2010)] have recently developed an indirect umbrella sampling (INDUS) method, that samples a coarse-grained particle number to obtain P(v)(N) in cuboidal volumes. Here, we present and demonstrate an extension of that approach to volumes of other basic shapes, like spheres and cylinders, as well as to collections of such volumes. We further describe the implementation of INDUS in the NPT ensemble and calculate P(v)(N) distributions over a broad range of pressures. Our method may be of particular interest in characterizing the hydrophobicity of interfaces of proteins, nanotubes and related systems.
Figures
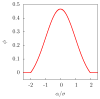


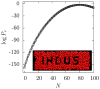

 = 1bar), with that obtained from NVT ensemble simulations having a buffering vapor-liquid interface located far from v.
= 1bar), with that obtained from NVT ensemble simulations having a buffering vapor-liquid interface located far from v.
Similar articles
-
Characterizing Solvent Density Fluctuations in Dynamical Observation Volumes.J Phys Chem B. 2019 Feb 21;123(7):1650-1661. doi: 10.1021/acs.jpcb.8b11423. Epub 2019 Feb 12. J Phys Chem B. 2019. PMID: 30682885
-
Sparse Sampling of Water Density Fluctuations in Interfacial Environments.J Chem Theory Comput. 2016 Feb 9;12(2):706-13. doi: 10.1021/acs.jctc.5b01037. Epub 2016 Jan 26. J Chem Theory Comput. 2016. PMID: 26745023
-
Connecting Non-Gaussian Water Density Fluctuations to the Lengthscale Dependent Crossover in Hydrophobic Hydration.J Phys Chem B. 2022 Oct 6;126(39):7604-7614. doi: 10.1021/acs.jpcb.2c04990. Epub 2022 Sep 26. J Phys Chem B. 2022. PMID: 36154059
-
Hydrophobicity of proteins and interfaces: insights from density fluctuations.Annu Rev Chem Biomol Eng. 2011;2:147-71. doi: 10.1146/annurev-chembioeng-061010-114156. Annu Rev Chem Biomol Eng. 2011. PMID: 22432614 Review.
-
Structural, electronic, optical and vibrational properties of nanoscale carbons and nanowires: a colloquial review.J Phys Condens Matter. 2010 Aug 25;22(33):334201. doi: 10.1088/0953-8984/22/33/334201. Epub 2010 Aug 4. J Phys Condens Matter. 2010. PMID: 21386491 Review.
Cited by
-
Molecular explanation for why talc surfaces can be both hydrophilic and hydrophobic.J Am Chem Soc. 2011 Dec 21;133(50):20521-7. doi: 10.1021/ja208687a. Epub 2011 Nov 23. J Am Chem Soc. 2011. PMID: 22035164 Free PMC article.
-
Solvation thermodynamics from cavity shapes of amino acids.PNAS Nexus. 2023 Jul 26;2(8):pgad239. doi: 10.1093/pnasnexus/pgad239. eCollection 2023 Aug. PNAS Nexus. 2023. PMID: 37545648 Free PMC article.
-
Extended surfaces modulate hydrophobic interactions of neighboring solutes.Proc Natl Acad Sci U S A. 2011 Oct 25;108(43):17678-83. doi: 10.1073/pnas.1110703108. Epub 2011 Oct 10. Proc Natl Acad Sci U S A. 2011. PMID: 21987795 Free PMC article.
-
Superhydrophilicity of α-alumina surfaces results from tight binding of interfacial waters to specific aluminols.J Colloid Interface Sci. 2022 Dec 15;628(Pt A):943-954. doi: 10.1016/j.jcis.2022.07.164. Epub 2022 Jul 30. J Colloid Interface Sci. 2022. PMID: 35964442 Free PMC article.
-
Sitting at the edge: how biomolecules use hydrophobicity to tune their interactions and function.J Phys Chem B. 2012 Mar 1;116(8):2498-503. doi: 10.1021/jp2107523. Epub 2012 Feb 16. J Phys Chem B. 2012. PMID: 22235927 Free PMC article.
References
Grants and funding
LinkOut - more resources
Full Text Sources
