Integrated cellular and gene interaction modelling of pattern formation
- PMID: 22199036
- PMCID: PMC4160909
- DOI: 10.1504/IJCBDD.2011.044444
Integrated cellular and gene interaction modelling of pattern formation
Abstract
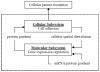
Cellular behaviour depends on and also modifies protein concentration and activity. An integrated cellular and gene interaction model is proposed to reveal this relationship. In this model, protein activity varies spatiotemporally with cellular location, gene interaction, and diffusion. In the meanwhile, cellular behaviour can vary spatially, driven by cell-cell signalling and inhomogeneous protein distribution across cells. This model integrates two components. The first component adopts a variation of the reaction-diffusion mechanism at the gene expression level. The second component is a lattice cellular model based on the Differential Adhesion Hypothesis (DAH) for cell sorting at the cellular level. Cell sorting and tumour invasion were simulated to illustrate the model. This model approximates cellular pattern formation more closely than existing models based on cell density.
Figures





Similar articles
-
Simulation of cell movement and interaction.J Bioinform Comput Biol. 2011 Feb;9(1):91-110. doi: 10.1142/s0219720011005318. J Bioinform Comput Biol. 2011. PMID: 21328708
-
A non-local evolution equation model of cell-cell adhesion in higher dimensional space.J Biol Dyn. 2013;7 Suppl 1(Suppl 1):68-87. doi: 10.1080/17513758.2012.755572. Epub 2013 Jan 7. J Biol Dyn. 2013. PMID: 23289870 Free PMC article.
-
BIO-LGCA: A cellular automaton modelling class for analysing collective cell migration.PLoS Comput Biol. 2021 Jun 15;17(6):e1009066. doi: 10.1371/journal.pcbi.1009066. eCollection 2021 Jun. PLoS Comput Biol. 2021. PMID: 34129639 Free PMC article.
-
Mathematical modelling in cell migration: tackling biochemistry in changing geometries.Biochem Soc Trans. 2020 Apr 29;48(2):419-428. doi: 10.1042/BST20190311. Biochem Soc Trans. 2020. PMID: 32239187 Review.
-
Rho family proteins in cell adhesion and cell migration.Eur J Cancer. 2000 Jun;36(10):1269-74. doi: 10.1016/s0959-8049(00)00091-5. Eur J Cancer. 2000. PMID: 10882865 Review.
References
-
- Agarwal P. Ph D dissertation. Dept of Computer Science, New York University; 1993. Cell-based computer models in developmental biology.
-
- Alexandrova AY. Evolution of cell interactions with extracellular matrix during carcinogenesis. Biochemistry (Moscow) 2008;73(No. 7):733–741. - PubMed
-
- Anderson ARA, Chaplain MAJ, Newman EL, Steele RJC, Thompson AM. Mathematical modeling of tumor invasion and metastasis. Journal of Theoretical Medicine. 2000;2:129–151.
-
- Bogenrieder T, Herlyn M. Axis of evil: molecular mechanisms of cancer metastasis. Oncogene. 2003;22:6524–6536. - PubMed
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
