Depth-dependent transverse shear properties of the human corneal stroma
- PMID: 22205608
- PMCID: PMC3317426
- DOI: 10.1167/iovs.11-8611
Depth-dependent transverse shear properties of the human corneal stroma
Abstract
Purpose: To measure the transverse shear modulus of the human corneal stroma and its profile through the depth by mechanical testing, and to assess the validity of the hypothesis that the shear modulus will be greater in the anterior third due to increased interweaving of lamellae.
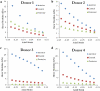
Methods: Torsional rheometry was used to measure the transverse shear properties of 6 mm diameter buttons of matched human cadaver cornea pairs. One cornea from each pair was cut into thirds through the thickness with a femtosecond laser and each stromal third was tested individually. The remaining intact corneas were tested to measure full stroma shear modulus. The shear modulus from a 1% shear strain oscillatory test was measured at various levels of axial compression for all samples.
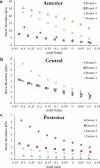
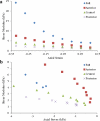
Results: After controlling for axial compression, the transverse shear moduli of isolated anterior layers were significantly higher than central and posterior layers. Mean modulus values at 0% axial strain were 7.71 ± 6.34 kPa in the anterior, 1.99 ± 0.45 kPa in the center, 1.31 ± 1.01 kPa in the posterior, and 9.48 ± 2.92 kPa for full thickness samples. A mean equilibrium compressive modulus of 38.7 ± 8.6 kPa at 0% axial strain was calculated from axial compression measured during the shear tests.
Conclusions: Transverse shear moduli are two to three orders of magnitude lower than tensile moduli reported in the literature. The profile of shear moduli through the depth displayed a significant increase from posterior to anterior. This gradient supports the hypothesis and corresponds to the gradient of interwoven lamellae seen in imaging of stromal cross-sections.
Figures

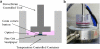



References
-
- Elsheikh A, Wang D, Brown M, Rama P, Campanelli M, Pye D. Assessment of corneal biomechanical properties and their variation with age. Curr Eye Res. 2007;32:11–19 - PubMed
-
- Elsheikh A, Brown M, Alhasso D, Rama P, Campanelli M, Garway-Heath D. Experimental assessment of corneal anisotropy. J Refract Surg. 2008;24:178–187 - PubMed
-
- Hjortdal JØ. Regional elastic performance of the human cornea. J Biomech. 1996;29:931–942 - PubMed
-
- Boyce BL, Grazier JM, Jones RE, Nguyen TD. Full-field deformation of bovine cornea under constrained inflation conditions. Biomaterials. 2008;29:3896–3904 - PubMed
-
- Christensen RM. Chapter 3.1: Transversely isotropic media. In: Mechanics of Composite Materials. 1st ed New York, NY: John Wiley & Sons; 1979:74–80
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

