Peripheral vision and pattern recognition: a review
- PMID: 22207654
- PMCID: PMC11073400
- DOI: 10.1167/11.5.13
Peripheral vision and pattern recognition: a review
Erratum in
-
Corrections to: Peripheral vision and pattern recognition: A review.J Vis. 2024 Apr 1;24(4):15. doi: 10.1167/jov.24.4.15. J Vis. 2024. PMID: 38630460 Free PMC article. No abstract available.
Abstract
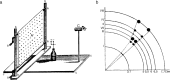
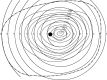
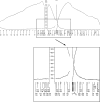
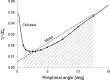
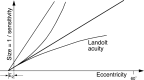
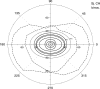
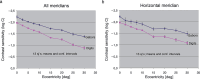
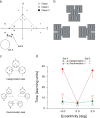
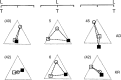
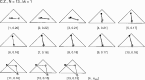
We summarize the various strands of research on peripheral vision and relate them to theories of form perception. After a historical overview, we describe quantifications of the cortical magnification hypothesis, including an extension of Schwartz's cortical mapping function. The merits of this concept are considered across a wide range of psychophysical tasks, followed by a discussion of its limitations and the need for non-spatial scaling. We also review the eccentricity dependence of other low-level functions including reaction time, temporal resolution, and spatial summation, as well as perimetric methods. A central topic is then the recognition of characters in peripheral vision, both at low and high levels of contrast, and the impact of surrounding contours known as crowding. We demonstrate how Bouma's law, specifying the critical distance for the onset of crowding, can be stated in terms of the retinocortical mapping. The recognition of more complex stimuli, like textures, faces, and scenes, reveals a substantial impact of mid-level vision and cognitive factors. We further consider eccentricity-dependent limitations of learning, both at the level of perceptual learning and pattern category learning. Generic limitations of extrafoveal vision are observed for the latter in categorization tasks involving multiple stimulus classes. Finally, models of peripheral form vision are discussed. We report that peripheral vision is limited with regard to pattern categorization by a distinctly lower representational complexity and processing speed. Taken together, the limitations of cognitive processing in peripheral vision appear to be as significant as those imposed on low-level functions and by way of crowding.
© ARVO
Figures










References
-
- Abbey, C. K., & Eckstein, M. P. (2002). Classification image analysis: Estimation and statistical inference for two-alternative forced-choice experiments. Journal of Vision, 2(1): 5, 66–78, http://www.journalofvision.org/content/2/1/5, doi:10.1167/2.1.5. [PubMed] [Article] - DOI - PubMed
-
- Adelson, E. H., & Bergen, J. R. (1985). Spatiotemporal energy models for the perception of motion. Journal of the Optical Society of America A, 2, 284–299. - PubMed
-
- Adler, J. S., Kripke, D. F., Loving, R. T., & Berga, S. L. (1992). Peripheral vision suppression of melatonin. Journal of Pineal Research, 12, 49–52. - PubMed
-
- Ahumada, A. J. Jr. (1996). Perceptual classification images from Vernier acuity masked by noise. Perception, 26, 18.
-
- Ahumada, A. J. Jr. (2002). Classification image weights and internal noise level estimation. Journal of Vision, 2(1): 8, 121–131, http://www.journalofvision.org/content/2/1/8, doi:10.1167/2.1.8. [PubMed] [Article] - DOI - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

