Probabilistic inference in general graphical models through sampling in stochastic networks of spiking neurons
- PMID: 22219717
- PMCID: PMC3240581
- DOI: 10.1371/journal.pcbi.1002294
Probabilistic inference in general graphical models through sampling in stochastic networks of spiking neurons
Abstract
An important open problem of computational neuroscience is the generic organization of computations in networks of neurons in the brain. We show here through rigorous theoretical analysis that inherent stochastic features of spiking neurons, in combination with simple nonlinear computational operations in specific network motifs and dendritic arbors, enable networks of spiking neurons to carry out probabilistic inference through sampling in general graphical models. In particular, it enables them to carry out probabilistic inference in Bayesian networks with converging arrows ("explaining away") and with undirected loops, that occur in many real-world tasks. Ubiquitous stochastic features of networks of spiking neurons, such as trial-to-trial variability and spontaneous activity, are necessary ingredients of the underlying computational organization. We demonstrate through computer simulations that this approach can be scaled up to neural emulations of probabilistic inference in fairly large graphical models, yielding some of the most complex computations that have been carried out so far in networks of spiking neurons.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
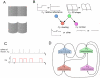
 . The relative reflectance (
. The relative reflectance ( ) of the two halves is either different (
) of the two halves is either different ( = 1) or the same (
= 1) or the same ( = 0). The perceived 3D shape can be cylindrical (
= 0). The perceived 3D shape can be cylindrical ( = 1) or flat (
= 1) or flat ( = 0). The relative reflectance and the 3D shape are direct causes of the shading (luminance change) of the surfaces (
= 0). The relative reflectance and the 3D shape are direct causes of the shading (luminance change) of the surfaces ( ), which can have the profile like in panel A (
), which can have the profile like in panel A ( = 1) or a different one (
= 1) or a different one ( = 0). The 3D shape of the surfaces causes different perceived contours, flat (
= 0). The 3D shape of the surfaces causes different perceived contours, flat ( = 0) or cylindrical (
= 0) or cylindrical ( = 1). The observed variables (evidence) are the contour (
= 1). The observed variables (evidence) are the contour ( ) and the shading (
) and the shading ( ). Subjects infer the marginal posterior probability distributions of the relative reflectance
). Subjects infer the marginal posterior probability distributions of the relative reflectance  and the 3D shape
and the 3D shape  based on the evidence. C) The RVs
based on the evidence. C) The RVs  are represented in our neural implementations by principal neurons
are represented in our neural implementations by principal neurons  . Each spike of
. Each spike of  sets the RV
sets the RV  to 1 for a time period of length
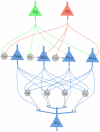
to 1 for a time period of length  . D) The structure of a network of spiking neurons that performs probabilistic inference for the Bayesian network of panel B through sampling from conditionals of the underlying distribution. Each principal neuron employs preprocessing to satisfy the NCC, either by dendritic processing or by a preprocessing circuit.
. D) The structure of a network of spiking neurons that performs probabilistic inference for the Bayesian network of panel B through sampling from conditionals of the underlying distribution. Each principal neuron employs preprocessing to satisfy the NCC, either by dendritic processing or by a preprocessing circuit.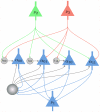
 and
and  in the Markov blanket of
in the Markov blanket of  . The principal neuron
. The principal neuron  (
( ) connects to the auxiliary neuron
) connects to the auxiliary neuron  directly if
directly if  (
( ) has value 1 in the assignment
) has value 1 in the assignment  , or via an inhibitory inter-neuron
, or via an inhibitory inter-neuron  if
if  (
( ) has value 0 in
) has value 0 in  . The auxiliary neurons connect with a strong excitatory connection to the principal neuron
. The auxiliary neurons connect with a strong excitatory connection to the principal neuron  , and drive it to fire whenever any one of them fires. The larger gray circle represents the lateral inhibition between the auxiliary neurons.
, and drive it to fire whenever any one of them fires. The larger gray circle represents the lateral inhibition between the auxiliary neurons.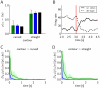
 (see (1)) is entered for the RVs
(see (1)) is entered for the RVs  and
and  , and the marginal probability
, and the marginal probability  is estimated. A) Target values of
is estimated. A) Target values of  for
for  and
and  are shown in black, results from sampling for
are shown in black, results from sampling for  from a network of spiking neurons are shown in green and blue. Panels C) and D) show the temporal evolution of the Kullback-Leibler divergence between the resulting estimates through neural sampling
from a network of spiking neurons are shown in green and blue. Panels C) and D) show the temporal evolution of the Kullback-Leibler divergence between the resulting estimates through neural sampling  and the correct posterior
and the correct posterior  , averaged over 10 trials for
, averaged over 10 trials for  in C) and for
in C) and for  in D). The green and blue areas around the green and blue curves represent the unbiased value of the standard deviation. The estimated marginal posterior is calculated for each time point from the samples (number of spikes) from the beginning of the simulation (or from
in D). The green and blue areas around the green and blue curves represent the unbiased value of the standard deviation. The estimated marginal posterior is calculated for each time point from the samples (number of spikes) from the beginning of the simulation (or from  for the second inference query with
for the second inference query with  ). Panels A, C, D show that both approaches yield correct probabilistic inference through neural sampling, but the approach via satisfying the NCC converges about 10 times faster. B) The firing rates of principal neuron
). Panels A, C, D show that both approaches yield correct probabilistic inference through neural sampling, but the approach via satisfying the NCC converges about 10 times faster. B) The firing rates of principal neuron  (solid line) and of the principal neuron
(solid line) and of the principal neuron  (dashed line) in the approach via satisfying the NCC, estimated with a sliding window (alpha kernel
(dashed line) in the approach via satisfying the NCC, estimated with a sliding window (alpha kernel  ). In this experiment the evidence
). In this experiment the evidence  was switched after 3 s (red vertical line) from
was switched after 3 s (red vertical line) from  to
to  . The “explaining away”effect is clearly visible from the complementary evolution of the firing rates of the neurons
. The “explaining away”effect is clearly visible from the complementary evolution of the firing rates of the neurons  and
and  .
.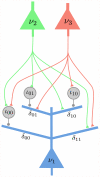
 has 4 dendritic branches, one for each possible assignment of values
has 4 dendritic branches, one for each possible assignment of values  to the RVs
to the RVs  and
and  in the Markov blanket of
in the Markov blanket of  . The dendritic branches of neuron
. The dendritic branches of neuron  receive synaptic inputs from the principal neurons
receive synaptic inputs from the principal neurons  and
and  either directly, or via an interneuron (analogously as in Fig. 2). It is required that at any moment in time exactly one of the dendritic branches (that one, whose index
either directly, or via an interneuron (analogously as in Fig. 2). It is required that at any moment in time exactly one of the dendritic branches (that one, whose index  agrees with the current firing states of
agrees with the current firing states of  and
and  ) generates dendritic spikes, whose amplitude at the soma determines the current firing probability of
) generates dendritic spikes, whose amplitude at the soma determines the current firing probability of  .
.
 for each possible value assignment
for each possible value assignment  to
to  and
and  . The connections from the neurons
. The connections from the neurons  and
and  (that carry the current values of the RVs
(that carry the current values of the RVs  and
and  ) to the auxiliary neurons are the same as in Fig. 2, and when these RVs change their value, the auxiliary neuron that corresponds to the new value fires. Each auxiliary neuron
) to the auxiliary neurons are the same as in Fig. 2, and when these RVs change their value, the auxiliary neuron that corresponds to the new value fires. Each auxiliary neuron  connects to the principal neuron
connects to the principal neuron  at a separate dendritic branch
at a separate dendritic branch  , and there is an inhibitory neuron
, and there is an inhibitory neuron  connecting to the same branch. The rest of the auxiliary neurons connect to the inhibitory interneuron
connecting to the same branch. The rest of the auxiliary neurons connect to the inhibitory interneuron  . The function of the inhibitory neuron
. The function of the inhibitory neuron  is to shunt the active EPSP caused by a recent spike from the auxiliary neuron
is to shunt the active EPSP caused by a recent spike from the auxiliary neuron  when the value of the
when the value of the  and
and  changes from
changes from  to another value.
to another value.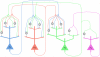
 occurs in two factors,
occurs in two factors,  and
and  , and therefore
, and therefore  receives synaptic inputs from
receives synaptic inputs from  and
and  on separate groups of dendritic branches. Altogether the synaptic connections of this network of spiking neurons implement the graph structure of Fig. 1D.
on separate groups of dendritic branches. Altogether the synaptic connections of this network of spiking neurons implement the graph structure of Fig. 1D.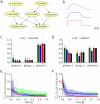
 from
from  to
to  (by clamping the x-ray test RV to 1). The probabilistic inference query is to estimate marginal posterior probabilities
(by clamping the x-ray test RV to 1). The probabilistic inference query is to estimate marginal posterior probabilities  ,
,  , and
, and  . A) The ASIA Bayesian network. B) The three different shapes of EPSPs, an alpha shape (green curve), a smooth plateau shape (blue curve) and the optimal rectangular shape (red curve). C) and D) Estimated marginal probabilities for each of the diseases, calculated from the samples generated during the first 800 ms of the simulation with alpha shaped (green bars), plateau shaped (blue bars) and rectangular (red bars) EPSPs, compared with the corresponding correct marginal posterior probabilities (black bars), for
. A) The ASIA Bayesian network. B) The three different shapes of EPSPs, an alpha shape (green curve), a smooth plateau shape (blue curve) and the optimal rectangular shape (red curve). C) and D) Estimated marginal probabilities for each of the diseases, calculated from the samples generated during the first 800 ms of the simulation with alpha shaped (green bars), plateau shaped (blue bars) and rectangular (red bars) EPSPs, compared with the corresponding correct marginal posterior probabilities (black bars), for  in C) and
in C) and  in D). The results are averaged over 20 simulations with different random initial conditions. The error bars show the unbiased estimate of the standard deviation. E) and F) The sum of the Kullback-Leibler divergences between the correct and the estimated marginal posterior probability for each of the diseases using alpha shaped (green curve), plateau shaped (blue curve) and rectangular (red curve) EPSPs, for
in D). The results are averaged over 20 simulations with different random initial conditions. The error bars show the unbiased estimate of the standard deviation. E) and F) The sum of the Kullback-Leibler divergences between the correct and the estimated marginal posterior probability for each of the diseases using alpha shaped (green curve), plateau shaped (blue curve) and rectangular (red curve) EPSPs, for  in E) and
in E) and  in F). The results are averaged over 20 simulation trials, and the light green and light blue areas show the unbiased estimate of the standard deviation for the green and blue curves respectively (the standard deviation for the red curve is not shown). The estimated marginal posteriors are calculated at each time point from the gathered samples from the beginning of the simulation (or from
in F). The results are averaged over 20 simulation trials, and the light green and light blue areas show the unbiased estimate of the standard deviation for the green and blue curves respectively (the standard deviation for the red curve is not shown). The estimated marginal posteriors are calculated at each time point from the gathered samples from the beginning of the simulation (or from  for the second inference query with
for the second inference query with  ).
).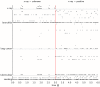
 to
to  (by clamping the RV X to 1). In each block of rows the lowest spike train shows the activity of a principal neuron (see left hand side for the label of the associated RV), and the spike trains above show the firing activity of the associated auxiliary neurons. After
(by clamping the RV X to 1). In each block of rows the lowest spike train shows the activity of a principal neuron (see left hand side for the label of the associated RV), and the spike trains above show the firing activity of the associated auxiliary neurons. After  the activity of the neurons for the x-ray test RV is not shown, since during this period the RV is clamped and the firing rate of its principal neuron is induced externally.
the activity of the neurons for the x-ray test RV is not shown, since during this period the RV is clamped and the firing rate of its principal neuron is induced externally.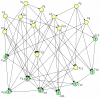
 is entered for nodes
is entered for nodes  in the lower part of the directed graph. The conditional probability tables were also randomly generated for all RVs.
in the lower part of the directed graph. The conditional probability tables were also randomly generated for all RVs.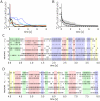
 , calculated from the generated samples (spikes) from the beginning of the simulation up to the current time indicated on the x-axis, for simulations with a neuron model with relative refractory period. Separate curves with different colors are shown for each of the 10 trials with different initial conditions (randomly chosen). The bold black curve corresponds to the simulation for which the spiking activity is shown in C) and D). B) As in A) but the mean over the 10 trials is shown, for simulations with a neuron model with relative refractory period (solid curve) and absolute refractory period (dashed curve.). The gray area around the solid curve shows the unbiased estimate of the standard deviation calculated over the 10 trials. C) and D) The spiking activity of the 12 principal neurons during the simulation from
, calculated from the generated samples (spikes) from the beginning of the simulation up to the current time indicated on the x-axis, for simulations with a neuron model with relative refractory period. Separate curves with different colors are shown for each of the 10 trials with different initial conditions (randomly chosen). The bold black curve corresponds to the simulation for which the spiking activity is shown in C) and D). B) As in A) but the mean over the 10 trials is shown, for simulations with a neuron model with relative refractory period (solid curve) and absolute refractory period (dashed curve.). The gray area around the solid curve shows the unbiased estimate of the standard deviation calculated over the 10 trials. C) and D) The spiking activity of the 12 principal neurons during the simulation from  to
to  , for one of the 10 simulations (neurons with relative refractory period). The neural network enters and remains in different network states (indicated by different colors), corresponding to different modes of the posterior probability distribution.
, for one of the 10 simulations (neurons with relative refractory period). The neural network enters and remains in different network states (indicated by different colors), corresponding to different modes of the posterior probability distribution.References
-
- Pearl J. Probabilistic Reasoning in Intelligent Systems. San Francisco, CA: Morgan- Kaufmann; 1988.
-
- Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neuroscience. 2007;30:535–574. - PubMed
-
- Grimmett GR, Stirzaker DR. Probability and Random Processes. 3rd edition. Oxford University Press; 2001.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

