Importance of factors determining the effective lifetime of a mass, long-lasting, insecticidal net distribution: a sensitivity analysis
- PMID: 22244509
- PMCID: PMC3273435
- DOI: 10.1186/1475-2875-11-20
Importance of factors determining the effective lifetime of a mass, long-lasting, insecticidal net distribution: a sensitivity analysis
Abstract
Background: Long-lasting insecticidal nets (LLINs) reduce malaria transmission by protecting individuals from infectious bites, and by reducing mosquito survival. In recent years, millions of LLINs have been distributed across sub-Saharan Africa (SSA). Over time, LLINs decay physically and chemically and are destroyed, making repeated interventions necessary to prevent a resurgence of malaria. Because its effects on transmission are important (more so than the effects of individual protection), estimates of the lifetime of mass distribution rounds should be based on the effective length of epidemiological protection.
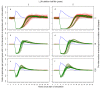
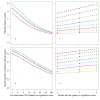
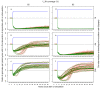
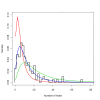
Methods: Simulation models, parameterised using available field data, were used to analyse how the distribution's effective lifetime depends on the transmission setting and on LLIN characteristics. Factors considered were the pre-intervention transmission level, initial coverage, net attrition, and both physical and chemical decay. An ensemble of 14 stochastic individual-based model variants for malaria in humans was used, combined with a deterministic model for malaria in mosquitoes.
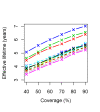
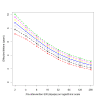
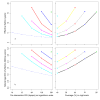
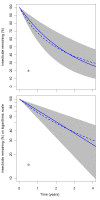
Results: The effective lifetime was most sensitive to the pre-intervention transmission level, with a lifetime of almost 10 years at an entomological inoculation rate of two infectious bites per adult per annum (ibpapa), but of little more than 2 years at 256 ibpapa. The LLIN attrition rate and the insecticide decay rate were the next most important parameters. The lifetime was surprisingly insensitive to physical decay parameters, but this could change as physical integrity gains importance with the emergence and spread of pyrethroid resistance.
Conclusions: The strong dependency of the effective lifetime on the pre-intervention transmission level indicated that the required distribution frequency may vary more with the local entomological situation than with LLIN quality or the characteristics of the distribution system. This highlights the need for malaria monitoring both before and during intervention programmes, particularly since there are likely to be strong variations between years and over short distances. The majority of SSA's population falls into exposure categories where the lifetime is relatively long, but because exposure estimates are highly uncertain, it is necessary to consider subsequent interventions before the end of the expected effective lifetime based on an imprecise transmission measure.
Figures













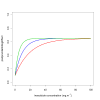

References
-
- WHO Global Malaria Programme. World Malaria Report 2010. Geneva: World Health Organization; 2010.
-
- Control of Neglected Tropical Diseases WHO Pesticide Evaluation Scheme, Global Malaria Programme Vector Control Unit. Guidelines for monitoring the durability of long-lasting insecticidal mosquito nets under operational conditions. Geneva: World Health Organization; 2011. WHO/HTM/NTD/WHOPES/2011.5.
-
- Kilian A. How long does a long-lasting insecticidal net last in the field? Public Health Journal. 2010;21:43–47.
-
- Hawley WA, Phillips-Howard P, ter Kuile F, Terlouw DJ, Vulule JM, Ombok M, Nahlen B, Gimnig JE, Kariuki SK, Kolczak MS, Hightower AW. Community-wide effects of permethrin-treated bed nets on child mortality and malaria morbidity in western Kenya. Am J Trop Med Hyg. 2003;68(Suppl. 4):121–127. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
Research Materials

