Intense or spatially heterogeneous predation can select against prey dispersal
- PMID: 22247764
- PMCID: PMC3256147
- DOI: 10.1371/journal.pone.0028924
Intense or spatially heterogeneous predation can select against prey dispersal
Abstract
Dispersal theory generally predicts kin competition, inbreeding, and temporal variation in habitat quality should select for dispersal, whereas spatial variation in habitat quality should select against dispersal. The effect of predation on the evolution of dispersal is currently not well-known: because predation can be variable in both space and time, it is not clear whether or when predation will promote dispersal within prey. Moreover, the evolution of prey dispersal affects strongly the encounter rate of predator and prey individuals, which greatly determines the ecological dynamics, and in turn changes the selection pressures for prey dispersal, in an eco-evolutionary feedback loop. When taken all together the effect of predation on prey dispersal is rather difficult to predict. We analyze a spatially explicit, individual-based predator-prey model and its mathematical approximation to investigate the evolution of prey dispersal. Competition and predation depend on local, rather than landscape-scale densities, and the spatial pattern of predation corresponds well to that of predators using restricted home ranges (e.g. central-place foragers). Analyses show the balance between the level of competition and predation pressure an individual is expected to experience determines whether prey should disperse or stay close to their parents and siblings, and more predation selects for less prey dispersal. Predators with smaller home ranges also select for less prey dispersal; more prey dispersal is favoured if predators have large home ranges, are very mobile, and/or are evenly distributed across the landscape.
Conflict of interest statement
Figures
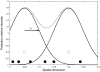
 , the spatial dispersion of the foraging effort distribution, is referred to in the main text as the predator home range size. On average, predators tend to kill more prey in the center of their home range so that prey progressively concentrate at predator home range boundaries; and this creates a negative spatial correlation between predator and prey distributions.
, the spatial dispersion of the foraging effort distribution, is referred to in the main text as the predator home range size. On average, predators tend to kill more prey in the center of their home range so that prey progressively concentrate at predator home range boundaries; and this creates a negative spatial correlation between predator and prey distributions.
 (upper row) and predation rate
(upper row) and predation rate  (lower row). White colouring indicates the mutant invades, and black that the mutant loses (does not invade). On the x-axis is represented the resident dispersal rate (
(lower row). White colouring indicates the mutant invades, and black that the mutant loses (does not invade). On the x-axis is represented the resident dispersal rate ( and on the y-axis the mutant dispersal rate (
and on the y-axis the mutant dispersal rate ( ). The ESS dispersal rate
). The ESS dispersal rate  is located at the intersection between black and white parts of the plane, along the diagonal. It is also convergence stable, in that it can be attained in a series of small ‘mutational’ steps. The first row shows that
is located at the intersection between black and white parts of the plane, along the diagonal. It is also convergence stable, in that it can be attained in a series of small ‘mutational’ steps. The first row shows that  increases with prey competition strength, while the second row shows
increases with prey competition strength, while the second row shows  to decrease with predation rate. Parameters held constant are
to decrease with predation rate. Parameters held constant are  . First row
. First row  , second row
, second row  . Here there are no post-natal predator movements (
. Here there are no post-natal predator movements ( ).
).
 (a–b–c) No feedbacks, one dimension.
(a–b–c) No feedbacks, one dimension.  . Uniform case,
. Uniform case,  , Segregated
, Segregated  , Aggregated
, Aggregated  . The values of the spatial autocorrelations are those that would have been obtained, if feedbacks were included (see below for the parameter values of predator demographic rates). (d–e–f) Demographic feedbacks, one dimension. Predator parameters
. The values of the spatial autocorrelations are those that would have been obtained, if feedbacks were included (see below for the parameter values of predator demographic rates). (d–e–f) Demographic feedbacks, one dimension. Predator parameters  . Specific parameters (d)
. Specific parameters (d)  (e)
(e)  (f)
(f)  (g–h–i) Two dimensions (no demography)
(g–h–i) Two dimensions (no demography)  .
.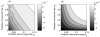
 and predator movement rate
and predator movement rate  ; and (b)as a function of average predator dispersal distance (
; and (b)as a function of average predator dispersal distance ( ) and predator movement rate
) and predator movement rate  . White indicates selection for dispersal (
. White indicates selection for dispersal ( , maximal value), and black against (
, maximal value), and black against ( ), while gray values around zero fitness are an intermediate zone where there actually is a positive ES dispersal rate (as shown in Figure 2). Parameters held constant are
), while gray values around zero fitness are an intermediate zone where there actually is a positive ES dispersal rate (as shown in Figure 2). Parameters held constant are  . In (a)
. In (a)  and in (b)
and in (b)  . Invasion fitness was computed using the moment approximation.
. Invasion fitness was computed using the moment approximation.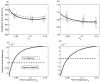
 ) non-dispersive type (resp. dispersive) is represented with a filled line (resp. a dashed line), both when the predator numerical response is absent (a) and present (b). In the lower panels, we show an index of the selective pressure for dispersal, the invasion fitness of a dispersive mutant (
) non-dispersive type (resp. dispersive) is represented with a filled line (resp. a dashed line), both when the predator numerical response is absent (a) and present (b). In the lower panels, we show an index of the selective pressure for dispersal, the invasion fitness of a dispersive mutant ( ) in a non-dispersive population (filled lines). The zero fitness value is shown with a horizontal dashed line, and separates selection against dispersal (below) versus selection for dispersal (above). The thin dotted line separates in all panel parameter regions selecting for and against dispersal. The case without a predator numerical response is presented in (c), while the numerical response is added in (d). Parameters:
) in a non-dispersive population (filled lines). The zero fitness value is shown with a horizontal dashed line, and separates selection against dispersal (below) versus selection for dispersal (above). The thin dotted line separates in all panel parameter regions selecting for and against dispersal. The case without a predator numerical response is presented in (c), while the numerical response is added in (d). Parameters:  . In the right column (b–d), additional predator parameters generating the demography take positive values;
. In the right column (b–d), additional predator parameters generating the demography take positive values;  . The solid lines are computed using the moment approximations, and the open circles and crosses in (a) and (b) are the landscape densities of prey averaged over 50 realisations of the IBM on a 1D line of length
. The solid lines are computed using the moment approximations, and the open circles and crosses in (a) and (b) are the landscape densities of prey averaged over 50 realisations of the IBM on a 1D line of length  .
.Similar articles
-
Conspecific density modulates the effect of predation on dispersal rates.Oecologia. 2015 Aug;178(4):1149-58. doi: 10.1007/s00442-015-3303-9. Epub 2015 Mar 29. Oecologia. 2015. PMID: 25820788
-
On the Fitness of Predators with Prey-Induced Dispersal in a Habitat with Spatial Heterogeneity.Bull Math Biol. 2022 Aug 31;84(10):111. doi: 10.1007/s11538-022-01069-5. Bull Math Biol. 2022. PMID: 36044077
-
Prey dispersal rate affects prey species composition and trait diversity in response to multiple predators in metacommunities.J Anim Ecol. 2010 Sep;79(5):1000-11. doi: 10.1111/j.1365-2656.2010.01715.x. Epub 2010 Jun 24. J Anim Ecol. 2010. PMID: 20584098
-
Habitat structure affects intraguild predation.Ecology. 2007 Nov;88(11):2713-9. doi: 10.1890/06-1408.1. Ecology. 2007. PMID: 18051638 Review.
-
Birds of prey as limiting factors of gamebird populations in Europe: a review.Biol Rev Camb Philos Soc. 2005 May;80(2):171-203. doi: 10.1017/s146479310400658x. Biol Rev Camb Philos Soc. 2005. PMID: 15921048 Review.
Cited by
-
Relative Preference and Localized Food Affect Predator Space Use and Consumption of Incidental Prey.PLoS One. 2016 Mar 15;11(3):e0151483. doi: 10.1371/journal.pone.0151483. eCollection 2016. PLoS One. 2016. PMID: 26978659 Free PMC article.
-
Population dynamics with spatial structure and an Allee effect.Proc Math Phys Eng Sci. 2020 Oct;476(2242):20200501. doi: 10.1098/rspa.2020.0501. Epub 2020 Oct 21. Proc Math Phys Eng Sci. 2020. PMID: 33223947 Free PMC article.
-
Colonization rates in a metacommunity altered by competition.PLoS One. 2014 Feb 13;9(2):e88344. doi: 10.1371/journal.pone.0088344. eCollection 2014. PLoS One. 2014. PMID: 24551094 Free PMC article.
-
Conspecific density modulates the effect of predation on dispersal rates.Oecologia. 2015 Aug;178(4):1149-58. doi: 10.1007/s00442-015-3303-9. Epub 2015 Mar 29. Oecologia. 2015. PMID: 25820788
References
-
- Johnson M, Gaines M. Evolution of dispersal: theoretical models and empirical tests using birds and mammals. Annu Rev Ecol Evol Syst. 1990;21:449–480.
-
- Bowler D, Benton T. Causes and consequences of animal dispersal strategies: relating individual behaviour to spatial dynamics. Biol Rev. 2005;80:205–225. - PubMed
-
- Ronce O. How does it feel to be like a rolling stone? Ten questions about dispersal evolution. Annu Rev Ecol Evol Syst. 2007;38:231–253.
-
- Hamilton W, May R. Dispersal in stable habitats. Nature. 1977;269:578–581.
-
- Holt R, McPeek M. Chaotic population dynamics favors the evolution of dispersal. Am Nat. 1996;148:709–718.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

