A three-dimensional model of an ultrasound contrast agent gas bubble and its mechanical effects on microvessels
- PMID: 22252221
- PMCID: PMC3367455
- DOI: 10.1088/0031-9155/57/3/785
A three-dimensional model of an ultrasound contrast agent gas bubble and its mechanical effects on microvessels
Abstract
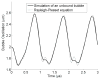
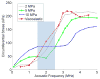
Ultrasound contrast agents inside a microvessel, when driven by ultrasound, oscillate and induce mechanical stresses on the vessel wall. These mechanical stresses can produce beneficial therapeutic effects but also induce vessel rupture if the stresses are too high. Therefore, it is important to use sufficiently low pressure amplitudes to avoid rupturing the vessels while still inducing the desired therapeutic effects. In this work, we developed a comprehensive three-dimensional model of a confined microbubble inside a vessel while considering the bubble shell properties, blood viscosity, vessel wall curvature and the mechanical properties of the vessel wall. Two bubble models with the assumption of a spherical symmetric bubble and a simple asymmetrical bubble were simulated. This work was validated with previous experimental results and enabled us to evaluate the microbubbles' behaviour and the resulting mechanical stresses induced on the vessel walls. In this study, the fluid shear and circumferential stresses were evaluated as indicators of the mechanical stresses. The effects of acoustical parameters, vessel viscoelasticity and rigidity, vessel/bubble size and off-centre bubbles on bubble behaviour and stresses on the vessel were investigated. The fluid shear and circumferential stresses acting on the vessel varied with time and location. As the frequency changed, the microbubble oscillated with the highest amplitude at its resonance frequency which was different from the resonance frequency of an unbound bubble. The bubble resonance frequency increased as the rigidity of a flexible vessel increased. The fluid shear and circumferential stresses peaked at frequencies above the bubble's resonance frequency. The more rigid the vessels were, the more damped the bubble oscillations. The synergistic effect of acoustic frequency and vessel elasticity had also been investigated since the circumferential stress showed either an increasing trend or a decreasing one versus the vessel rigidity at different acoustic frequencies. When the acoustic pressure was increased from 52 to 680 kPa, the maximum bubble radius increase by 2.5 fold, and the maximum shear and circumferential stress increased by 15.7 and 18.3 fold, respectively. The shear stress was largest when the acoustic frequency was higher (3.25 MHz) and the ratio of the vessel radius to the bubble radius was lower. The circumferential stress was largest when the bubble wall was closer to the vessel wall. An oscillating off-centre bubble forms a mushroom shape with the most damping on the points closest to the vessel wall.
Figures






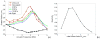






References
-
- Bao S, Thrall BD, Gies RA, Miller DL. In vivo transfection of melanoma cells by lithotripter shock waves. Cancer Research. 1998;58:219–221. - PubMed
-
- Becher H, Burns PN. Handbook of contrast echocardiography : left ventrical function and myocardial perfusion. Springer Verlag; 2000.
-
- Brujan EA, Nahen K, Schmidt P, Vogel A. Dynamics of laser-induced cavitation bubbles near an elastic boundary. J Fluid Mech. 2001;433:251–281.
-
- Caskey CF, Kruse DE, Dayton PA, Kitano TK, Ferrara KW. Microbubble oscillation in tubes with diameters of 12, 25, and 195 microns. Appl Phys Lett. 2006;88:033902.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
