Observation of the inverse spin Hall effect in silicon

Abstract

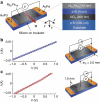
The spin-orbit interaction in a solid couples the spin of an electron to its momentum. This coupling gives rise to mutual conversion between spin and charge currents: the direct and inverse spin Hall effects. The spin Hall effects have been observed in metals and semiconductors. However, the spin/charge conversion has not been realized in one of the most fundamental semiconductors, silicon, where accessing the spin Hall effects has been believed to be difficult because of its very weak spin-orbit interaction. Here we report observation of the inverse spin Hall effect in silicon at room temperature. The spin/charge current conversion efficiency, the spin Hall angle, is obtained as 0.0001 for a p-type silicon film. In spite of the small spin Hall angle, we found a clear electric voltage due to the inverse spin Hall effect in the p-Si film, demonstrating that silicon can be used as a spin-current detector.

Figure 1. Experimental set-up.

(a) A schematic illustration of the Ni₈₁Fe₁₉/p-Si film used in this study. H represents an external magnetic field. (b) Current-voltage (I–V) characteristic measured for the Ni₈₁Fe₁₉/p-Si film, where the two electrodes are attached to the AuPd layers. w_F is the length of the Ni₈₁Fe₁₉ layer. (c) I–V characteristic measured for the Ni₈₁Fe₁₉/p-Si film. The two electrodes are attached to the Ni₈₁Fe₁₉ layer and AuPd layer, respectively.

Figure 2. Observation of ISHE in silicon.

(a) Field (H) dependence of the electromotive force V measured for the Ni₈₁Fe₁₉/p-Si film when θ=0 at different microwave excitation powers. The external magnetic field is applied along the film plane. Here the background voltage due to the microwave irradiation is subtracted from the V spectra. The inset shows a schematic illustration of the experimental set-up when θ=0. (b) H dependence of V measured for the Ni₈₁Fe₁₉/p-Si film when θ=180° at different microwave excitation powers. (c) H dependence of the FMR signal dI(H)/dH measured for the Ni₈₁Fe₁₉/p-Si film when θ=0 at 200 mW microwave excitation (see the inset to a). I is the microwave absorption intensity. The solid circles are the experimental data. The solid curve shows the fitting result using the first derivative of a Lorentz function. (d) H dependence of dI(H)/dH for the Ni₈₁Fe₁₉/p-Si film when θ=180° at 200 mW microwave excitation (see the inset to b). (e) H dependence of V for the Ni₈₁Fe₁₉/p-Si film when θ=0. The solid circles are the experimental data. The solid curve shows the fitting result using with the parameters V_s=3.50 μV and V_as=−0.41 μV. (f) H dependence of V measured for the Ni₈₁Fe₁₉/p-Si film when θ=180°. The solid curve shows the fitting result with the parameters V_s=1.76 μV and V_as=0.41 μV. (g) The spectral shape of the symmetric V_s (H) and asymmetric V_as (H) components of the electromotive force V (H). (h) Microwave power P_MW dependence of ΔV_s, where . The solid circles are the experimental data. The solid line shows the linear fit to the data.

Figure 3. Angular dependence of ISHE signal and spin precession.

(a) A schematic illustration of the Ni₈₁Fe₁₉/p-Si film when the external magnetic field H is applied oblique to the film plane. M denotes the static component of the magnetization. θ and φ show the magnetic field angle and magnetization angle, respectively. (b) Magnetic field angle θ dependence of the FMR field H_FMR measured for the Ni₈₁Fe₁₉/p-Si film. The filled circles represent the experimental data. The solid curve is the numerical solution of the Landau–Lifshitz–Gilbert equation with the saturation magnetization 4πM_s=0.852T. (c) Magnetic field angle θ dependence of the magnetization angle φ for the Ni₈₁Fe₁₉/p-Si film estimated using the Landau–Lifshitz–Gilbert equation with the measured values of H_FMR. (d) Magnetic field angle θ dependence of the FMR signal dI(H)/dH measured for the Ni₈₁Fe₁₉/p-Si film at 200 mW. (e) Magnetic field angle θ dependence of the symmetric component of the electromotive force V_s (H) extracted by a fitting procedure from the measured V spectra for the Ni₈₁Fe₁₉/p-Si film at 200 mW. (f) Magnetic field angle θ dependence of ΔV_s. The solid circles are the experimental data. The solid curve is the theoretical curve obtained from equation (5) with τ_sf=9 ps. The dashed curve is the theoretical curve for τ_sf=0. The error bars represent the 90% confidence interval. The inset shows the θ dependence of ΔV_s calculated from equation (5) with τ_sf=20 ps (the red curve), τ_sf=10 ps (the blue curve), and (the black curve).

Figure 4. Spin current relaxation.

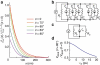
(a) The spin current density generated by the spin pumping for τ_sf=9 ps. Here is the spin current density at the interface when the external magnetic field is applied along the film plane (θ=0). The parameters used for the calculation are shown in the text. (b) An equivalent circuit model of the Ni₈₁Fe₁₉/p-Si film. R_F is the electrical resistance of the Ni₈₁Fe₁₉ layer. (c) A simplified equivalent circuit model of the Ni₈₁Fe₁₉/p-Si film. (d) The spin relaxation time τ_sf dependence of the ISHE signal V_ISHE at θ=80° calculated from equation (5).