Navigation as a source of geometric knowledge: young children's use of length, angle, distance, and direction in a reorientation task
- PMID: 22257573
- PMCID: PMC3306253
- DOI: 10.1016/j.cognition.2011.12.015
Navigation as a source of geometric knowledge: young children's use of length, angle, distance, and direction in a reorientation task
Abstract
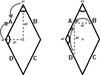
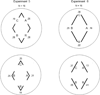
Geometry is one of the highest achievements of our species, but its foundations are obscure. Consistent with longstanding suggestions that geometrical knowledge is rooted in processes guiding navigation, the present study examines potential sources of geometrical knowledge in the navigation processes by which young children establish their sense of orientation. Past research reveals that children reorient both by the shape of the surface layout and the shapes of distinctive landmarks, but it fails to clarify what shape properties children use. The present study explores 2-year-old children's sensitivity to angle, length, distance and direction by testing disoriented children's search in a variety of fragmented rhombic and rectangular environments. Children reoriented themselves in accord with surface distances and directions, but they failed to use surface lengths or corner angles either for directional reorientation or as local landmarks. Thus, navigating children navigate by some but not all of the abstract properties captured by formal Euclidean geometry. While navigation systems may contribute to children's developing geometric understanding, they likely are not the sole source of abstract geometric intuitions.
Copyright © 2011 Elsevier B.V. All rights reserved.
Figures



References
-
- Biederman I, Cooper EE. Size invariance in visual object priming. Journal of Experimental Psychology: Human Perception and Performance. 1992;18:121–133.
-
- Brown AA, Spetch ML, Hurd PL. Growing in circles: Rearing environment alters spatial navigation in fish. Psychological Science. 2007;18:569–573. - PubMed
-
- Burgess N. Spatial memory: How egocentric and allocentric combine. Trends in Cognitive Sciences. 2006;10:551–557. - PubMed
-
- Burgess N. Spatial cognition and the brain. Annals of the New York Academy of Sciences. 2008;1124:77–97. - PubMed
-
- Cheng K. A purely geometric module in the rats’ spatial representation. Cognition. 1986;23:149–178. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

