Evaluating the physiological significance of respiratory sinus arrhythmia: looking beyond ventilation-perfusion efficiency
- PMID: 22289913
- PMCID: PMC3573317
- DOI: 10.1113/jphysiol.2011.222422
Evaluating the physiological significance of respiratory sinus arrhythmia: looking beyond ventilation-perfusion efficiency
Abstract
We conducted a theoretical study of the physiological significance of respiratory sinus arrhythmia (RSA), a phenomenon used as an index of cardiac vagal tone and wellbeing, whereby the heart rate (HR) increases during inspiration and decreases during expiration. We first tested the hypothesis that RSA improves gas exchange efficiency but found that although gas exchange efficiency improved with slow and deep breathing and with increased mean heart rate, this was unrelated to RSA. We then formulated and tested a new hypothesis: that RSA minimizes the work done by the heart while maintaining physiological levels of arterial carbon dioxide. We tested the new hypothesis using two methods. First, the HR for which the work is minimized was calculated using techniques from optimal control theory. This calculation was done on simplified models that we derived from a previously published model of gas exchange in mammals. We found that the calculated HR was remarkably similar to RSA and that this became more profound under slow and deep breathing. Second, the HR was prescribed and the work done by the heart was calculated by conducting a series of numerical experiments on the previously published gas exchange model. We found that cardiac work was minimized for RSA-like HR functions, most profoundly under slow and deep breathing. These findings provide novel insights into potential reasons for and benefits of RSA under physiological conditions.
Figures
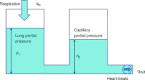

 ) was constrained to 104 mmHg, the averaged arterial partial pressure of CO2 (
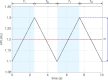
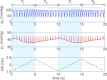
) was constrained to 104 mmHg, the averaged arterial partial pressure of CO2 ( ) was constrained to 41 mmHg, and VT= 0.5 l. All other parameters are the same as in Appendix A. Heart rate (HR) calculated for Model 1a – continuous line, HR calculated for Model 1b – dashed line. TI and TE are the inspiration and expiration periods, respectively. Note that O2 and CO2 are uncoupled.
) was constrained to 41 mmHg, and VT= 0.5 l. All other parameters are the same as in Appendix A. Heart rate (HR) calculated for Model 1a – continuous line, HR calculated for Model 1b – dashed line. TI and TE are the inspiration and expiration periods, respectively. Note that O2 and CO2 are uncoupled.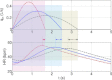
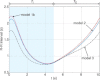
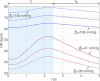


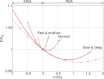

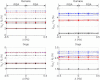

 where n= 2 (dashed line), n= 1.5 (continuous line) or n= 3 (dashed–dotted line) and by using Model 1b.
where n= 2 (dashed line), n= 1.5 (continuous line) or n= 3 (dashed–dotted line) and by using Model 1b.References
-
- Anrep GV, Pascual W, Rossler R. Respiratory variations of the heart rate. II. The central mechanism of the respiratory arrhythmia and the inter-relations between the central and the reflex mechanisms. Proc Royal Soc Lond B Biol Sci. 1936;119:218–230.
-
- Batzel JJ, Schneditz D, Tran TH. Cardiovascular and Respiratory Systems: Modeling, Analysis, and Control. Philadelphia: Society for Industrial and Applied Mathematics; 2007.
-
- Ben-Tal A. Simplified models for gas exchange in the human lungs. J Theor Biol. 2006;238:474–495. - PubMed
-
- Calder WA., 3rd Scaling of physiological processes in homeothermic animals. Annu Rev Physiol. 1981;43:301–322. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

