Uncovering spatial topology represented by rat hippocampal population neuronal codes
- PMID: 22307459
- PMCID: PMC3974406
- DOI: 10.1007/s10827-012-0384-x
Uncovering spatial topology represented by rat hippocampal population neuronal codes
Abstract
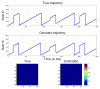
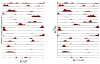
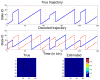
Hippocampal population codes play an important role in representation of spatial environment and spatial navigation. Uncovering the internal representation of hippocampal population codes will help understand neural mechanisms of the hippocampus. For instance, uncovering the patterns represented by rat hippocampus (CA1) pyramidal cells during periods of either navigation or sleep has been an active research topic over the past decades. However, previous approaches to analyze or decode firing patterns of population neurons all assume the knowledge of the place fields, which are estimated from training data a priori. The question still remains unclear how can we extract information from population neuronal responses either without a priori knowledge or in the presence of finite sampling constraint. Finding the answer to this question would leverage our ability to examine the population neuronal codes under different experimental conditions. Using rat hippocampus as a model system, we attempt to uncover the hidden "spatial topology" represented by the hippocampal population codes. We develop a hidden Markov model (HMM) and a variational Bayesian (VB) inference algorithm to achieve this computational goal, and we apply the analysis to extensive simulation and experimental data. Our empirical results show promising direction for discovering structural patterns of ensemble spike activity during periods of active navigation. This study would also provide useful insights for future exploratory data analysis of population neuronal codes during periods of sleep.
Figures




Similar articles
-
Neural representation of spatial topology in the rodent hippocampus.Neural Comput. 2014 Jan;26(1):1-39. doi: 10.1162/NECO_a_00538. Epub 2013 Oct 8. Neural Comput. 2014. PMID: 24102128 Free PMC article.
-
A Bayesian nonparametric approach for uncovering rat hippocampal population codes during spatial navigation.J Neurosci Methods. 2016 Apr 1;263:36-47. doi: 10.1016/j.jneumeth.2016.01.022. Epub 2016 Feb 5. J Neurosci Methods. 2016. PMID: 26854398 Free PMC article.
-
A variational nonparametric Bayesian approach for inferring rat hippocampal population codes.Annu Int Conf IEEE Eng Med Biol Soc. 2013;2013:7092-5. doi: 10.1109/EMBC.2013.6611192. Annu Int Conf IEEE Eng Med Biol Soc. 2013. PMID: 24111379
-
Directing place representation in the hippocampus.Rev Neurosci. 2001;12(4):347-63. doi: 10.1515/revneuro.2001.12.4.347. Rev Neurosci. 2001. PMID: 11783719 Review.
-
Simulation of spatial learning in the Morris water maze by a neural network model of the hippocampal formation and nucleus accumbens.Hippocampus. 1995;5(3):171-88. doi: 10.1002/hipo.450050304. Hippocampus. 1995. PMID: 7550613 Review.
Cited by
-
How our understanding of memory replay evolves.J Neurophysiol. 2023 Mar 1;129(3):552-580. doi: 10.1152/jn.00454.2022. Epub 2023 Feb 8. J Neurophysiol. 2023. PMID: 36752404 Free PMC article. Review.
-
Neural representation of spatial topology in the rodent hippocampus.Neural Comput. 2014 Jan;26(1):1-39. doi: 10.1162/NECO_a_00538. Epub 2013 Oct 8. Neural Comput. 2014. PMID: 24102128 Free PMC article.
-
Gamma Synchronization Influences Map Formation Time in a Topological Model of Spatial Learning.PLoS Comput Biol. 2016 Sep 16;12(9):e1005114. doi: 10.1371/journal.pcbi.1005114. eCollection 2016 Sep. PLoS Comput Biol. 2016. PMID: 27636199 Free PMC article.
-
An overview of Bayesian methods for neural spike train analysis.Comput Intell Neurosci. 2013;2013:251905. doi: 10.1155/2013/251905. Epub 2013 Nov 17. Comput Intell Neurosci. 2013. PMID: 24348527 Free PMC article. Review.
-
Topological Schemas of Memory Spaces.Front Comput Neurosci. 2018 Apr 24;12:27. doi: 10.3389/fncom.2018.00027. eCollection 2018. Front Comput Neurosci. 2018. PMID: 29740306 Free PMC article.
References
-
- Amari S, Ozeki T, Park HY. Learning and inference in hierarchical models with singularities. Systems and Computers in Japan. 2003;34(7):34–42.
-
- Baum LE, Petrie T, Soules G, Weiss N. A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains. Annals of Mathematical Statistics. 1970;41(1):164–171.
-
- Beal MJ, Ghahramani Z, Rasmussen CE. Advances in Neural Information Processing Systems. MIT Press; 2002. The infinite hidden Markov model; p. 14.
-
- Beal MJ. PhD Thesis. Gatsby Computational Neuroscience Unit, University College London; 2003. Variational algorithms for approximate Bayesian inference.
-
- Bellman R. Dynamic Programming. Princeton University Press; Boston: 1957.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

