Loss tangent and complex modulus estimated by acoustic radiation force creep and shear wave dispersion

Abstract

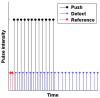
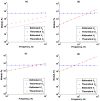
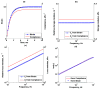
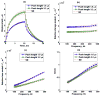
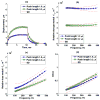
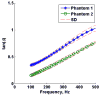
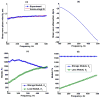
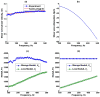
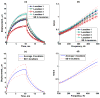
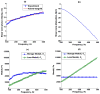
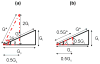
Elasticity imaging methods have been used to study tissue mechanical properties and have demonstrated that tissue elasticity changes with disease state. In current shear wave elasticity imaging methods typically only shear wave speed is measured and rheological models, e.g. Kelvin-Voigt, Maxwell and Standard Linear Solid, are used to solve for tissue mechanical properties such as the shear viscoelastic complex modulus. This paper presents a method to quantify viscoelastic material properties in a model-independent way by estimating the complex shear elastic modulus over a wide frequency range using time-dependent creep response induced by acoustic radiation force. This radiation force induced creep method uses a conversion formula that is the analytic solution of a constitutive equation. The proposed method in combination with shearwave dispersion ultrasound vibrometry is used to measure the complex modulus so that knowledge of the applied radiation force magnitude is not necessary. The conversion formula is shown to be sensitive to sampling frequency and the first reliable measure in time according to numerical simulations using the Kelvin-Voigt model creep strain and compliance. Representative model-free shear complex moduli from homogeneous tissue mimicking phantoms and one excised swine kidney were obtained. This work proposes a novel model-free ultrasound-based elasticity method that does not require a rheological model with associated fitting requirements.

Figure 1

Illustration of the pulse sequences used to induce and monitor creep and recovery. The symbols represent pushing beams (●), detecting beams (*) and reference beams (△).

Figure 2

Kelvin-Voigt model creep compliance for a shear elastic modulus, G, of 6 kPa and viscosity, η, of 2 Pa·s (-) and 10 Pa·s (-*). The time vector in (a) starts at t₁ of 1 ms with a sampling rate, F_s, of 1 kHz. The time vector in (b) starts at t₁ of 0.1 ms with a sampling rate of 10 kHz.

Figure 3

Estimated and theoretical storage modulus (-, *), G_s, and loss modulus (--, o), G_l, as a function of frequency from Kelvin-Voigt model creep compliance for shear elastic modulus, G, of 6 kPa and viscosity, η, of 2 Pa·s and (a) sampling frequency, F_s, of 1 kHz, (b) sampling frequency, F_s, of 10 kHz. Viscosity, η, of 10 Pa·s and (c) sampling frequency, F_s, of 1 kHz, (d) sampling frequency, F_s, of 10 kHz.

Figure 4

Kelvin-Voigt model; (a) creep strain (o) and creep compliance (-) response of shear elastic modulus, G, of 6 kPa, and viscosity, η, of 6 Pa·s at 10 kHz sampling rate. (b) Estimated relative storage modulus from creep strain (o), C_s, and creep compliance (-), G_s. (c) Estimated relative loss modulus from creep strain, C_l, and creep compliance, G_l. (d) tan(δ) from estimated complex modulus using from creep strain (o) and creep compliance (-).

Figure 5

Kelvin-Voigt model tan(δ) for (a) fixed viscosity, η, at 10 Pa·s and shear elastic modulus, G, of 6 kPa (-), 9 kPa (*) and 12 kPa (o) at 10 kHz sampling rate; (b) fixed shear elastic modulus, G, at 9 kPa and viscosity, η, of 2 Pa·s (-), 4 Pa·s (*) and 6 Pa·s (o) at 10 kHz sampling rate.

Figure 6

Phantom 1 (a) mean creep displacement, (b) estimated relative storage moduli, C_s, (c) estimated relative loss moduli, C_l, and (d) loss tangent, tan(δ), of a 1.6 μs (o) and 3.2 μs (*) push duration. Average of 5 repeated measurements over a window of 3 mm in axial direction and 1 mm in lateral direction. The dashed lines represent the standard deviation of 5 repeated measurements.

Figure 7

Phantom 2 (a) mean creep displacement, (b) estimated relative storage moduli, C_s, (c) estimated relative loss moduli, C_l, and (d) loss tangent, tan(δ), of a 1.6 μs (o) and 3.2 μs (*) push duration. Average of 5 repeated measurements over a window of 3 mm in axial direction and 1 mm in lateral direction. The dashed lines represent the standard deviation of 5 repeated measurements.

Figure 8

Loss tangent (average of 5 measured locations using 3.2 μs push duration) as a function of frequency for phantom 1 (*) and phantom 2 (o). The dashed lines represent the standard deviation of 5 measured locations in each phantom.

Figure 9

Phantom 1 (a) shear wave speed dispersion estimated by SDUV, (b) shear wave attenuation estimated by SDUV and RFIC, (c) model-free complex moduli estimated by shear wave phase velocity and shear wave attenuation, (d) complex moduli estimated by Kelvin-Voigt model fit to SDUV shear wave speed dispersion.

Figure 10

Phantom 2 (a) shear wave speed dispersion estimated by SDUV, (b) shear wave attenuation estimated by SDUV and RFIC, (c) model-free complex moduli estimated by shear wave phase velocity and shear wave attenuation, (d) complex moduli estimated by Kelvin-Voigt model fit to SDUV shear wave speed dispersion.

Figure 11

Excised swine kidney (a) mean creep displacement, (b) estimated loss tangent of 5 repeated measurements in 4 locations, the dashed lines represent the standard deviation of 5 repeated measurements. (c) Mean creep displacement and (d) loss tangent of 5 locations, dashed lines represent the standard deviation of 4 locations.

Figure 12

Excised swine kidney (a) shear wave speed dispersion estimated by SDUV, (b) shear wave attenuation estimated by SDUV and RFIC, (c) complex moduli estimated by shear wave phase velocity and shear wave attenuation, (d) complex moduli estimated by Kelvin-Voigt model fit to SDUV shear wave speed dispersion.

Figure 13

Vector diagrams of the relationship between loss angle, δ, complex modulus, G^*, storage modulus, G_s, and loss modulus, G_l. The complex modulus, G^*, is independent of tan(δ) when G_s and G_l change independently; (a) changing G_s and G_l in opposite direction cause tan(δ) to change and G^* remains the same; (b) changing G_s and G_l in the same direction and magnitude causes G^* to change but tan(δ) remains the same.