Graph fission in an evolving voter model

Abstract

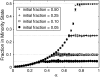
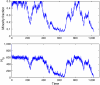
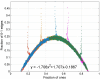
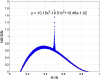
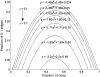
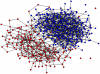
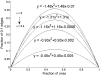
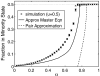
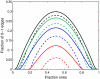
We consider a simplified model of a social network in which individuals have one of two opinions (called 0 and 1) and their opinions and the network connections coevolve. Edges are picked at random. If the two connected individuals hold different opinions then, with probability 1 - α, one imitates the opinion of the other; otherwise (i.e., with probability α), the link between them is broken and one of them makes a new connection to an individual chosen at random (i) from those with the same opinion or (ii) from the network as a whole. The evolution of the system stops when there are no longer any discordant edges connecting individuals with different opinions. Letting ρ be the fraction of voters holding the minority opinion after the evolution stops, we are interested in how ρ depends on α and the initial fraction u of voters with opinion 1. In case (i), there is a critical value α(c) which does not depend on u, with ρ ≈ u for α > α(c) and ρ ≈ 0 for α < α(c). In case (ii), the transition point α(c)(u) depends on the initial density u. For α > α(c)(u), ρ ≈ u, but for α < α(c)(u), we have ρ(α,u) = ρ(α,1/2). Using simulations and approximate calculations, we explain why these two nearly identical models have such dramatically different phase transitions.

Fig. 1.

Simulation results for rewire-to-same model, starting from Erdös–Rényi graphs with N = 100,000 nodes and average degree λ = 4.

Fig. 2.

Simulation results for the rewire-to-random model, starting from Erdös–Rényi graphs with N = 100,000 nodes and average degree λ = 4.

Fig. 3.

Fraction of nodes with the minority opinion (min{N₀,N₁}/N) and the number of discordant edges N₁₀ versus time, for a simulation of N = 1,000 nodes, u = 0.5, and α = 0.3.

Fig. 4.

Plot of N₁₀/M versus N₁/N when α = 0.5 in the rewire-to-random case. Five simulations starting from u = 0.2, 0.35, 0.5, 0.65, and 0.8 are plotted in different colors. These results are from graphs with N = 10,000 vertices and plotted every 1,000 steps.

Fig. 5.

Plot of N₀₁₀/N versus N₁/N when α = 0.5 in the rewire-to-random case. All simulations start at u = 0.5 because multiple runs from one starting point are enough to explore all of the arch. These results are from graphs with N = 100,000 vertices and plotted every 10,000 steps.

Fig. 6.

Observed arches for the rewire-to-random model. The specified parabolas are fits to simulation data with N = 10,000, λ = 4.

Fig. 7.

Visualization of the rewire-to-random model soon before fission occurs, for N = 500 nodes, average degree λ = 4, and α = 0.65. Colors correspond to the two opinions.

Fig. 8.

Observed arches for rewire-to-same model. The specified parabolas are fits to simulation data with N = 10,000, λ = 4.

Fig. 9.

Predictions of the ending minority fraction ρ(α) in rewire-to-random case from pair approximation (dashed line) and approximate master equation (solid line), compared with simulation (x).

Fig. 10.

Arches computed by approximate master equation (solid lines) versus simulation (dashes) for rewire-to-random model with α = 0.4, 0.5, 0.6, 0.7. The curves decrease as α increases.