Reconsidering association testing methods using single-variant test statistics as alternatives to pooling tests for sequence data with rare variants

Abstract

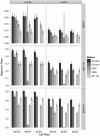
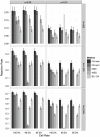
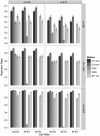
Association tests that pool minor alleles into a measure of burden at a locus have been proposed for case-control studies using sequence data containing rare variants. However, such pooling tests are not robust to the inclusion of neutral and protective variants, which can mask the association signal from risk variants. Early studies proposing pooling tests dismissed methods for locus-wide inference using nonnegative single-variant test statistics based on unrealistic comparisons. However, such methods are robust to the inclusion of neutral and protective variants and therefore may be more useful than previously appreciated. In fact, some recently proposed methods derived within different frameworks are equivalent to performing inference on weighted sums of squared single-variant score statistics. In this study, we compared two existing methods for locus-wide inference using nonnegative single-variant test statistics to two widely cited pooling tests under more realistic conditions. We established analytic results for a simple model with one rare risk and one rare neutral variant, which demonstrated that pooling tests were less powerful than even Bonferroni-corrected single-variant tests in most realistic situations. We also performed simulations using variants with realistic minor allele frequency and linkage disequilibrium spectra, disease models with multiple rare risk variants and extensive neutral variation, and varying rates of missing genotypes. In all scenarios considered, existing methods using nonnegative single-variant test statistics had power comparable to or greater than two widely cited pooling tests. Moreover, in disease models with only rare risk variants, an existing method based on the maximum single-variant Cochran-Armitage trend chi-square statistic in the locus had power comparable to or greater than another existing method closely related to some recently proposed methods. We conclude that efficient locus-wide inference using single-variant test statistics should be reconsidered as a useful framework for devising powerful association tests in sequence data with rare variants.

Figure 1. MAF and within-gene pairwise LD distributions in actual sequence data.

Distributions of MAFs (Panel A) and within-gene pairwise LD (Panel B) for biallelic variants in six candidate genes for dilated cardiomyopathy. Pairwise LD was measured by the correlation coefficient (r) between major/minor alleles for variants within the same gene. These distributions were estimated from 184 Coriell samples of European descent. The vertical dashed line in Panel B indicates r = 0.

Figure 2. Analytic power comparisons in a small sample (N = 500).

Analytic locus-wide power at α = 0.05 of the BC-CA (lower bound), collapsing, and summing tests at a locus comprising one neutral and one risk variant as a function of the pairwise correlation coefficient between major/minor alleles (r). The variants had the same MAF = 0.005 (Panel A) or MAF = 0.01 (Panel B), and the relative risk was 3 (Panel A) or 2 (Panel B) for each additional minor allele at the risk variant. Both panels assume penetrance of 0.05 for the major allele homozygote at the risk variant and a balanced case-control sample with N = 500 total subjects.

Figure 3. Simulated type I error rate comparison.

Monte Carlo estimates of rejection rates for each association testing procedure based on 1,000 samples from a null disease model with no risk variants. Estimates are reported by call rate, nominal α level, and sample size (N). Error bars represent exact binomial 95% confidence intervals for the rejection rate, and dashed horizontal lines are included at the nominal α level. The CMC could not be performed at a call rate of 95% because no individual had complete genotype data in any sample; at a call rate of 99.5%, CMC results with F ddf>4 were available in 23, 619, and 992 samples for N = 500, 1,000, and 2,000, respectively.

Figure 4. Simulated power comparison for rare risk variants (MAF<0.005; OR = 3).

Monte Carlo estimates of rejection rates for each association testing procedure based on 1,000 samples from a disease model with 50 rare risk variants (MAF<0.005; OR = 3), which represent ∼5% of all variants in the locus in the average population. Estimates are reported by call rate, nominal α level, and sample size (N). Error bars represent exact binomial 95% confidence intervals for the rejection rate. The CMC could not be performed at a call rate of 95% because no individual had complete genotype data in any sample; at a call rate of 99.5%, CMC results with F ddf>4 were available in 22, 596, and 991 samples for N = 500, 1,000, and 2,000, respectively.

Figure 5. Simulated power comparison for rare risk variants (MAF<0.01; OR = 2).

Monte Carlo estimates of rejection rates for each association testing procedure based on 1,000 samples from a disease model with 50 rare risk variants (MAF<0.01; OR = 2), which represent ∼5% of all variants in the locus in the average population. Estimates are reported by call rate, nominal α level, and sample size (N). Error bars represent exact binomial 95% confidence intervals for the rejection rate. The CMC could not be performed at a call rate of 95% because no individual had complete genotype data in any sample; at a call rate of 99.5%, CMC results with F ddf>4 were available in 18, 573, and 986 samples for N = 500, 1,000, and 2,000, respectively.

Figure 6. Simulated power comparison for a mixture of rare and common risk variants.

Monte Carlo estimates of rejection rates for each association testing procedure based on 1,000 samples from a disease model with 50 total risk variants, which represent ∼5% of all variants in the locus in the average population, randomly allocated between rare variants (MAF<0.01; OR = 2), low-frequency variants (0.01≤MAF<0.05; OR = 1.5), and common variants (0.05≤MAF<0.10; OR = 1.2). Estimates are reported by call rate, nominal α level, and sample size (N). Error bars represent exact binomial 95% confidence intervals for the rejection rate. The CMC could not be performed at a call rate of 95% because no individual had complete genotype data in any sample; at a call rate of 99.5%, CMC results with F ddf>4 were available in 15, 564, and 989 samples for N = 500, 1,000, and 2,000, respectively.