A symmetric dual feedback system provides a robust and entrainable oscillator
- PMID: 22363442
- PMCID: PMC3282687
- DOI: 10.1371/journal.pone.0030489
A symmetric dual feedback system provides a robust and entrainable oscillator
Abstract
Many organisms have evolved molecular clocks to anticipate daily changes in their environment. The molecular mechanisms by which the circadian clock network produces sustained cycles have extensively been studied and transcriptional-translational feedback loops are common structures to many organisms. Although a simple or single feedback loop is sufficient for sustained oscillations, circadian clocks implement multiple, complicated feedback loops. In general, different types of feedback loops are suggested to affect the robustness and entrainment of circadian rhythms. To reveal the mechanism by which such a complex feedback system evolves, we quantify the robustness and light entrainment of four competing models: the single, semi-dual, dual, and redundant feedback models. To extract the global properties of those models, all plausible kinetic parameter sets that generate circadian oscillations are searched to characterize their oscillatory features. To efficiently perform such analyses, we used the two-phase search (TPS) method as a fast and non-biased search method and quasi-multiparameter sensitivity (QMPS) as a fast and exact measure of robustness to uncertainty of all kinetic parameters.So far the redundant feedback model has been regarded as the most robust oscillator, but our extensive analysis corrects or overcomes this hypothesis. The dual feedback model, which is employed in biology, provides the most robust oscillator to multiple parameter perturbations within a cell and most readily entrains to a wide range of light-dark cycles. The kinetic symmetry between the dual loops and their coupling via a protein complex are found critically responsible for robust and entrainable oscillations. We first demonstrate how the dual feedback architecture with kinetic symmetry evolves out of many competing feedback systems.
Conflict of interest statement
Figures




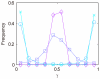
 , where [X(nuc)]mean indicates the mean concentration for X in nucleus and [Y(nuc)]mean that for Y in nucleus. When γ is close to zero, the effect of the X loop on the oscillator is weak, while the Y loop is dominant. When γ is close to 0.5, the effects of both the X and Y loops are comparable. When γ is close to one, the X loop is dominant. At ρ = 0 (perfect kinetic symmetry), γ is always equal to 0.5. The distribution for ρ = 0 is not shown.
, where [X(nuc)]mean indicates the mean concentration for X in nucleus and [Y(nuc)]mean that for Y in nucleus. When γ is close to zero, the effect of the X loop on the oscillator is weak, while the Y loop is dominant. When γ is close to 0.5, the effects of both the X and Y loops are comparable. When γ is close to one, the X loop is dominant. At ρ = 0 (perfect kinetic symmetry), γ is always equal to 0.5. The distribution for ρ = 0 is not shown.
Similar articles
-
Analytical study of robustness of a negative feedback oscillator by multiparameter sensitivity.BMC Syst Biol. 2014;8 Suppl 5(Suppl 5):S1. doi: 10.1186/1752-0509-8-S5-S1. Epub 2014 Dec 12. BMC Syst Biol. 2014. PMID: 25605374 Free PMC article.
-
A reduced model clarifies the role of feedback loops and time delays in the Drosophila circadian oscillator.Biophys J. 2002 Nov;83(5):2349-59. doi: 10.1016/S0006-3495(02)75249-1. Biophys J. 2002. PMID: 12414672 Free PMC article.
-
Mathematical identification of critical reactions in the interlocked feedback model.PLoS One. 2007 Oct 31;2(10):e1103. doi: 10.1371/journal.pone.0001103. PLoS One. 2007. PMID: 17971866 Free PMC article.
-
Network switches and their role in circadian clocks.J Biol Chem. 2024 May;300(5):107220. doi: 10.1016/j.jbc.2024.107220. Epub 2024 Mar 22. J Biol Chem. 2024. PMID: 38522517 Free PMC article. Review.
-
Role of posttranscriptional regulation in circadian clocks: lessons from Drosophila.Chronobiol Int. 1999 Jul;16(4):377-414. doi: 10.3109/07420529908998716. Chronobiol Int. 1999. PMID: 10442235 Review.
Cited by
-
Coupling protocol of interlocked feedback oscillators in circadian clocks.J R Soc Interface. 2020 Jun;17(167):20200287. doi: 10.1098/rsif.2020.0287. Epub 2020 Jun 3. J R Soc Interface. 2020. PMID: 32486952 Free PMC article.
-
Systematic analysis of negative and positive feedback loops for robustness and temperature compensation in circadian rhythms.NPJ Syst Biol Appl. 2023 Feb 11;9(1):5. doi: 10.1038/s41540-023-00268-7. NPJ Syst Biol Appl. 2023. PMID: 36774353 Free PMC article.
-
Analysis of the spiking dynamics of a diode laser with dual optical feedback.Sci Rep. 2025 Jan 9;15(1):1391. doi: 10.1038/s41598-025-85876-5. Sci Rep. 2025. PMID: 39789207 Free PMC article.
-
Robustness analysis of the detailed kinetic model of an ErbB signaling network by using dynamic sensitivity.PLoS One. 2017 May 24;12(5):e0178250. doi: 10.1371/journal.pone.0178250. eCollection 2017. PLoS One. 2017. PMID: 28542548 Free PMC article.
-
Analytical study of robustness of a negative feedback oscillator by multiparameter sensitivity.BMC Syst Biol. 2014;8 Suppl 5(Suppl 5):S1. doi: 10.1186/1752-0509-8-S5-S1. Epub 2014 Dec 12. BMC Syst Biol. 2014. PMID: 25605374 Free PMC article.
References
-
- Dunlap JC. Molecular bases for circadian clocks. Cell. 1999;96:271–290. - PubMed
-
- Goldbeter A. A model for circadian oscillations in the Drosophila period protein (PER). Proc Biol Sci. 1995;261:319–324. - PubMed
-
- Leloup JC, Goldbeter A. A model for circadian rhythms in Drosophila incorporating the formation of a complex between the PER and TIM proteins. J Biol Rhythms. 1998;13:70–87. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

