Efficient exact maximum a posteriori computation for bayesian SNP genotyping in polyploids
- PMID: 22363513
- PMCID: PMC3281906
- DOI: 10.1371/journal.pone.0030906
Efficient exact maximum a posteriori computation for bayesian SNP genotyping in polyploids
Abstract
The problem of genotyping polyploids is extremely important for the creation of genetic maps and assembly of complex plant genomes. Despite its significance, polyploid genotyping still remains largely unsolved and suffers from a lack of statistical formality. In this paper a graphical bayesian model for SNP genotyping data is introduced. This model can infer genotypes even when the ploidy of the population is unknown. We also introduce an algorithm for finding the exact maximum a posteriori genotype configuration with this model. This algorithm is implemented in a freely available web-based software package SuperMASSA. We demonstrate the utility, efficiency, and flexibility of the model and algorithm by applying them to two different platforms, each of which is applied to a polyploid data set: Illumina GoldenGate data from potato and Sequenom MassARRAY data from sugarcane. Our method achieves state-of-the-art performance on both data sets and can be trivially adapted to use models that utilize prior information about any platform or species.
Conflict of interest statement
Figures
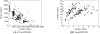
 depend on the genotypes of all individuals
depend on the genotypes of all individuals  . In both models the distribution of genotypes
. In both models the distribution of genotypes  is determined by the genotype configuration
is determined by the genotype configuration  . Also, in both models the probability of a genotype distribution depends on
. Also, in both models the probability of a genotype distribution depends on  , the distribution of genotypes in the population. Furthermore, both models use the same method to compute the probability of the data given the genotype configuration. Lastly, the possible genotypes depend on the ploidy
, the distribution of genotypes in the population. Furthermore, both models use the same method to compute the probability of the data given the genotype configuration. Lastly, the possible genotypes depend on the ploidy  . (A) In the Hardy-Weinberg model, the distribution of genotypes in the population is determined by one of the allele frequencies
. (A) In the Hardy-Weinberg model, the distribution of genotypes in the population is determined by one of the allele frequencies  . (B) In the
. (B) In the  model, the distribution of genotypes in the population depends on the parent genotypes
model, the distribution of genotypes in the population depends on the parent genotypes  and
and  . The dashed arrows and nodes (
. The dashed arrows and nodes ( and
and  ) depict optional dependencies and variables; these variables and dependencies exist only when data from the parents is included.
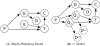
) depict optional dependencies and variables; these variables and dependencies exist only when data from the parents is included.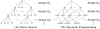
 , searching through genotype configurations can be viewed as a tree in which each individual genotype assignment branches into
, searching through genotype configurations can be viewed as a tree in which each individual genotype assignment branches into  separate outcomes. (A) A naive search progresses downward through the tree and chooses the series of genotype assignments that lead to the highest posterior probability. A naive branch and bound method derived from this tree bounds genotype configurations for which the prefix determines that all subsequent paths are poor. (B) A multinomial graph ( i.e. the subset graph of the power-set of G) merges outcomes that result in the same genotype counts
separate outcomes. (A) A naive search progresses downward through the tree and chooses the series of genotype assignments that lead to the highest posterior probability. A naive branch and bound method derived from this tree bounds genotype configurations for which the prefix determines that all subsequent paths are poor. (B) A multinomial graph ( i.e. the subset graph of the power-set of G) merges outcomes that result in the same genotype counts  . Multiple paths (from the top) can lead to any given set of genotype counts; therefore, dynamic programming is used. Given the layer above, each node can compute the most likely path from the top that leads to it. Once the most likely path and score are computed for each node in a layer, the next layer can progress. At the bottom layer, the node with the highest combined likelihood
. Multiple paths (from the top) can lead to any given set of genotype counts; therefore, dynamic programming is used. Given the layer above, each node can compute the most likely path from the top that leads to it. Once the most likely path and score are computed for each node in a layer, the next layer can progress. At the bottom layer, the node with the highest combined likelihood  (computed via dynamic programming) and
(computed via dynamic programming) and  (the same for any path terminating at the node) maximizes the posterior probability. As in the naive tree, once all lower adjacent nodes in a subtree are provably suboptimal, then the subtree can be bounded. The dynamic programming approach is substantially more time space-efficient than the naive approach.
(the same for any path terminating at the node) maximizes the posterior probability. As in the naive tree, once all lower adjacent nodes in a subtree are provably suboptimal, then the subtree can be bounded. The dynamic programming approach is substantially more time space-efficient than the naive approach.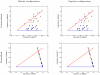
 and
and  within the likelihood function
within the likelihood function  . The two figures on the left correspond to a suboptimal genotype configuration. In the figures on the right, a pair of “blue” and “red” points (highlighted) are switched to the opposite class. After swapping the categories, the numbers of individuals with each genotype
. The two figures on the left correspond to a suboptimal genotype configuration. In the figures on the right, a pair of “blue” and “red” points (highlighted) are switched to the opposite class. After swapping the categories, the numbers of individuals with each genotype  do not change, but the total distance between these two points and their classes decreases. Decreasing this distance increases the likelihood while holding
do not change, but the total distance between these two points and their classes decreases. Decreasing this distance increases the likelihood while holding  constant. Thus the joint probability
constant. Thus the joint probability  . Because the MAP configuration cannot be improved by any such swaps, it must correspond to contiguous groups of class assignments along the normalized axis. Searching only the configurations that result in contiguous class assignments dramatically narrows the search space and makes inference computationally feasible where it wouldn't be with the dynamic programming branch and bound method.
. Because the MAP configuration cannot be improved by any such swaps, it must correspond to contiguous groups of class assignments along the normalized axis. Searching only the configurations that result in contiguous class assignments dramatically narrows the search space and makes inference computationally feasible where it wouldn't be with the dynamic programming branch and bound method.
 . Both methods were implemented in Python and run on sugarcane locus SugSNP225 and timed using user time. Parental data was not used. For this data set, the optimal ploidy and
. Both methods were implemented in Python and run on sugarcane locus SugSNP225 and timed using user time. Parental data was not used. For this data set, the optimal ploidy and  values are
values are  . In the figure on the left,
. In the figure on the left,  is held constant at
is held constant at  and the ploidy is varied from 2 to 10. In the figure on the right, the ploidy is fixed at 10 and
and the ploidy is varied from 2 to 10. In the figure on the right, the ploidy is fixed at 10 and  is doubled successively from
is doubled successively from  to
to  . In both figures, the dynamic programming branch and bound series is incomplete because the method was terminated after using more than 3 GB of RAM. In comparison, the geometric branch and bound method never used more than 50 MB. The growing gap between the methods indicates a superpolynomial speedup, especially when larger ploidies and larger values of
. In both figures, the dynamic programming branch and bound series is incomplete because the method was terminated after using more than 3 GB of RAM. In comparison, the geometric branch and bound method never used more than 50 MB. The growing gap between the methods indicates a superpolynomial speedup, especially when larger ploidies and larger values of  are used. For very low
are used. For very low  values, the dynamic programming method is sometimes slightly faster due to decreased overhead.
values, the dynamic programming method is sometimes slightly faster due to decreased overhead.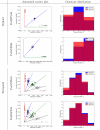
 .
.
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

