Epidemiological models of Mycobacterium tuberculosis complex infections
- PMID: 22387570
- PMCID: PMC3330831
- DOI: 10.1016/j.mbs.2012.02.003
Epidemiological models of Mycobacterium tuberculosis complex infections
Abstract
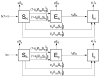
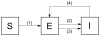
The resurgence of tuberculosis in the 1990s and the emergence of drug-resistant tuberculosis in the first decade of the 21st century increased the importance of epidemiological models for the disease. Due to slow progression of tuberculosis, the transmission dynamics and its long-term effects can often be better observed and predicted using simulations of epidemiological models. This study provides a review of earlier study on modeling different aspects of tuberculosis dynamics. The models simulate tuberculosis transmission dynamics, treatment, drug resistance, control strategies for increasing compliance to treatment, HIV/TB co-infection, and patient groups. The models are based on various mathematical systems, such as systems of ordinary differential equations, simulation models, and Markov Chain Monte Carlo methods. The inferences from the models are justified by case studies and statistical analysis of TB patient datasets.
Copyright © 2012 Elsevier Inc. All rights reserved.
Figures
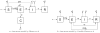
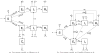
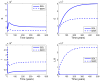
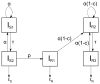
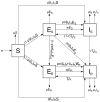
References
-
- WHO. Report, Global tuberculosis control : epidemiology, strategy, financing. Geneva: World Health Organization; 2009.
-
- Colijn C, Cohen T, Murray M. Mathematical Models of Tuberculosis: accomplishments and future challenges. Proceedings of BIOMAT International Symposium on Mathematical and Computational Biology; World Scientific Publisher; 2006. pp. 123–148.
-
- Aparicio JP, Capurro AF, Castillo-Chavez C. Transmission and dynamics of tuberculosis on generalized households. Journal of Theoretical Biology. 2000;206:327– 341. - PubMed
-
- Snider GL. Tuberculosis then and now: A personal perspective on the last 50 years. Annals of Internal Medicine. 1997;126:237–243. - PubMed
-
- CDC. Reported Tuberculosis in the United States, 2008. Sep, 2009.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

