Filtered FCS: species auto- and cross-correlation functions highlight binding and dynamics in biomolecules
- PMID: 22407544
- PMCID: PMC3495305
- DOI: 10.1002/cphc.201100897
Filtered FCS: species auto- and cross-correlation functions highlight binding and dynamics in biomolecules
Abstract
An analysis method of lifetime, polarization and spectrally filtered fluorescence correlation spectroscopy, referred to as filtered FCS (fFCS), is introduced. It uses, but is not limited to, multiparameter fluorescence detection to differentiate between molecular species with respect to their fluorescence lifetime, polarization and spectral information. Like the recently introduced fluorescence lifetime correlation spectroscopy (FLCS) [Chem. Phys. Lett. 2002, 353, 439-445], fFCS is based on pulsed laser excitation. However, it uses the species-specific polarization and spectrally resolved fluorescence decays to generate filters. We determined the most efficient method to generate global filters taking into account the anisotropy information. Thus, fFCS is able to distinguish species, even if they have very close or the same fluorescence lifetime, given differences in other fluorescence parameters. fFCS can be applied as a tool to compute species-specific auto- (SACF) and cross- correlation (SCCF) functions from a mixture of different species for accurate and quantitative analysis of their concentration, diffusion and kinetic properties. The computed correlation curves are also free from artifacts caused by unspecific background signal. We tested this methodology by simulating the extreme case of ligand-receptor binding processes monitored only by differences in fluorescence anisotropy. Furthermore, we apply fFCS to an experimental single-molecule FRET study of an open-to-closed conformational transition of the protein Syntaxin-1. In conclusion, fFCS and the global analysis of the SACFs and SCCF is a key tool to investigate binding processes and conformational dynamics of biomolecules in a nanosecond-to-millisecond time range as well as to unravel the involved molecular states.
Copyright © 2012 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim.
Figures

 as a case imitating single detection channel experiment). The same decay pattern is used for both detection channels and correspondingly the same filters are applied for parallel and perpendicular detection channels to mimic the one detector case. The correlations show poor statistics with some degree of separation between species. B) scenario 2: SACF from Equation (12) using two detectors, independent filter generation for each detection channel and stacking them afterwards. The separation is better compared to the single detector case. C) SACF of scenario 3 using Equation (12) for two detectors and global filter generation. The separation of species is obvious to the eye, and the estimated error in the recovered parameters is within 2 %. A detail error analysis of recovered parameters is done in Section 2.2.
as a case imitating single detection channel experiment). The same decay pattern is used for both detection channels and correspondingly the same filters are applied for parallel and perpendicular detection channels to mimic the one detector case. The correlations show poor statistics with some degree of separation between species. B) scenario 2: SACF from Equation (12) using two detectors, independent filter generation for each detection channel and stacking them afterwards. The separation is better compared to the single detector case. C) SACF of scenario 3 using Equation (12) for two detectors and global filter generation. The separation of species is obvious to the eye, and the estimated error in the recovered parameters is within 2 %. A detail error analysis of recovered parameters is done in Section 2.2.
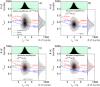
 with a fundamental anisotropy r0=0.375 and the species-specific rotational correlation times ρ. A) 50 by 50 percent (X(LR)=0.5) mixture of static species. B) 80 by 20 percent (X(LR)=0.2) mixture of dynamic species (k1,2=2000 s−1; k2,1=8000 s−1 or tR=0.1 ms), C) 50 by 50 percent (X(LR)=0.5) mixture of dynamic species (k1,2=k2,1=2000 s−1 or tR=0.25 ms). D) 20 by 80 percent (X(LR)=0.8) mixture of dynamic species (k1,2=8000 s−1; k2,1=2000 s−1 or tR=0.1 ms). The 1D lifetime τG distributions are overlaid by corresponding ones from 50 by 50 percent static mixture (green line). The 1D rsc,G distributions (gray) are overlaid by distributions from 100 % free ligand (blue line), 50 by 50 percent mixture of static species (green line) and 100 % complex (red line).
with a fundamental anisotropy r0=0.375 and the species-specific rotational correlation times ρ. A) 50 by 50 percent (X(LR)=0.5) mixture of static species. B) 80 by 20 percent (X(LR)=0.2) mixture of dynamic species (k1,2=2000 s−1; k2,1=8000 s−1 or tR=0.1 ms), C) 50 by 50 percent (X(LR)=0.5) mixture of dynamic species (k1,2=k2,1=2000 s−1 or tR=0.25 ms). D) 20 by 80 percent (X(LR)=0.8) mixture of dynamic species (k1,2=8000 s−1; k2,1=2000 s−1 or tR=0.1 ms). The 1D lifetime τG distributions are overlaid by corresponding ones from 50 by 50 percent static mixture (green line). The 1D rsc,G distributions (gray) are overlaid by distributions from 100 % free ligand (blue line), 50 by 50 percent mixture of static species (green line) and 100 % complex (red line).
 and
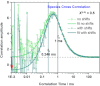
and  . The background signal consists of dark counts=0.2 kHz and scatter=1.8 kHz. The filtered FCS curves were computed by using the filters generated from polarization-resolved decays shown in Figure 2. Comparison of FCCS, SACFs and fit curves for the following cases: A) Overlay of FCCS curves calculated from raw simulated data for 50/50 % static (gray) and 50/50 % dynamic mixtures (green). B) Overlay of SACFs for 50/50 % mixtures: static and dynamic equilibrium, respectively, with (k1,2=k2,1=2000 s−1 or tR=0.25 ms). C) Overlay of SACFs for 20/80 % mixtures: static and dynamic equilibrium, respectively, with (k1,2=8000 s−1, k2,1=2000 s−1 or tR=0.1 ms). D) Overlay of SCCFs for two cases: i) 50/50 % mixtures: static (gray curve) and dynamic (green curve, k1,2=k2,1=2000 s−1 or tR=0.25 ms) equilibrium (fit results to tR=0.246 ms); ii) 80/20 % mixture in a dynamic equilibrium (pink curve, k1,2=2000 s−1, k2,1=8000 s−1 or tR=0.1 ms). The fit gave tR=0.096 ms; iii) 20/80 % mixture in a dynamic equilibrium (blue curve, k1,2=8000 s−1, k2,1=2000 s−1 or tR=0.1 ms). The fit results in tR=0.099 ms.
. The background signal consists of dark counts=0.2 kHz and scatter=1.8 kHz. The filtered FCS curves were computed by using the filters generated from polarization-resolved decays shown in Figure 2. Comparison of FCCS, SACFs and fit curves for the following cases: A) Overlay of FCCS curves calculated from raw simulated data for 50/50 % static (gray) and 50/50 % dynamic mixtures (green). B) Overlay of SACFs for 50/50 % mixtures: static and dynamic equilibrium, respectively, with (k1,2=k2,1=2000 s−1 or tR=0.25 ms). C) Overlay of SACFs for 20/80 % mixtures: static and dynamic equilibrium, respectively, with (k1,2=8000 s−1, k2,1=2000 s−1 or tR=0.1 ms). D) Overlay of SCCFs for two cases: i) 50/50 % mixtures: static (gray curve) and dynamic (green curve, k1,2=k2,1=2000 s−1 or tR=0.25 ms) equilibrium (fit results to tR=0.246 ms); ii) 80/20 % mixture in a dynamic equilibrium (pink curve, k1,2=2000 s−1, k2,1=8000 s−1 or tR=0.1 ms). The fit gave tR=0.096 ms; iii) 20/80 % mixture in a dynamic equilibrium (blue curve, k1,2=8000 s−1, k2,1=2000 s−1 or tR=0.1 ms). The fit results in tR=0.099 ms.



 ) for each species as described in Equation (26). The IRF shape is shown in gray. The first species (blue line) has ρ(1)=0.1 ns and the second species (red line) has ρ(2)=0.3 ns. B) The generated filters for each species (
) for each species as described in Equation (26). The IRF shape is shown in gray. The first species (blue line) has ρ(1)=0.1 ns and the second species (red line) has ρ(2)=0.3 ns. B) The generated filters for each species ( ) are plotted according to the notation: IRF shown in gray, species 1 in blue, and species 2 in red. C) The independently normalized TCSPC histograms for species 1 and 2 according to Equation (27). D) Simultaneously independently minimized filters using Equations (29) and (30). E) Conditional probabilities for each species as described in Equations (4)–(6). The IRF shape is shown in gray. The first species has a rotational correlation of ρ(1)=0.1 ns and its decay is shown in blue. The second species with rotational correlation ρ(2)=0.3 ns is shown in red. F) The filters generated for each species (
) are plotted according to the notation: IRF shown in gray, species 1 in blue, and species 2 in red. C) The independently normalized TCSPC histograms for species 1 and 2 according to Equation (27). D) Simultaneously independently minimized filters using Equations (29) and (30). E) Conditional probabilities for each species as described in Equations (4)–(6). The IRF shape is shown in gray. The first species has a rotational correlation of ρ(1)=0.1 ns and its decay is shown in blue. The second species with rotational correlation ρ(2)=0.3 ns is shown in red. F) The filters generated for each species ( ) according to Equations (10) and (11) are plotted. The IRF filter is shown in gray, species 1 in blue, and species 2 in red.
) according to Equations (10) and (11) are plotted. The IRF filter is shown in gray, species 1 in blue, and species 2 in red.References
-
- Magde D, Elson EL, Webb WW. Phys. Rev. Lett. 1972;29:705–708.
-
- Rigler R, Foldes-Papp Z, Meyer-Almes FJ, Sammet C, Volcker M, Schnetz A. J. Biotechnol. 1998;63:97–109. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

