Construction and validation of anisotropic and orthotropic ventricular geometries for quantitative predictive cardiac electrophysiology
- PMID: 22419977
- PMCID: PMC3262240
- DOI: 10.1098/rsfs.2010.0005
Construction and validation of anisotropic and orthotropic ventricular geometries for quantitative predictive cardiac electrophysiology
Abstract
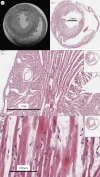
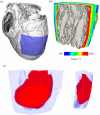
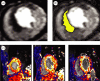
Reaction-diffusion computational models of cardiac electrophysiology require both dynamic excitation models that reconstruct the action potentials of myocytes as well as datasets of cardiac geometry and architecture that provide the electrical diffusion tensor D, which determines how excitation spreads through the tissue. We illustrate an experimental pipeline we have developed in our laboratories for constructing and validating such datasets. The tensor D changes with location in the myocardium, and is determined by tissue architecture. Diffusion tensor magnetic resonance imaging (DT-MRI) provides three eigenvectors e(i) and eigenvalues λ(i) at each voxel throughout the tissue that can be used to reconstruct this architecture. The primary eigenvector e(1) is a histologically validated measure of myocyte orientation (responsible for anisotropic propagation). The secondary and tertiary eigenvectors (e(2) and e(3)) specify the directions of any orthotropic structure if λ(2) is significantly greater than λ(3)-this orthotropy has been identified with sheets or cleavage planes. For simulations, the components of D are scaled in the fibre and cross-fibre directions for anisotropic simulations (or fibre, sheet and sheet normal directions for orthotropic tissues) so that simulated conduction velocities match values from optical imaging or plunge electrode experiments. The simulated pattern of propagation of action potentials in the models is partially validated by optical recordings of spatio-temporal activity on the surfaces of hearts. We also describe several techniques that enhance components of the pipeline, or that allow the pipeline to be applied to different areas of research: Q ball imaging provides evidence for multi-modal orientation distributions within a fraction of voxels, infarcts can be identified by changes in the anisotropic structure-irregularity in myocyte orientation and a decrease in fractional anisotropy, clinical imaging provides human ventricular geometry and can identify ischaemic and infarcted regions, and simulations in human geometries examine the roles of anisotropic and orthotropic architecture in the initiation of arrhythmias.
Keywords: cardiac arrhythmia; computational modelling; diffusion tensor magnetic resonance imaging; myocardium; optical imaging.
Figures
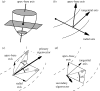
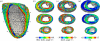
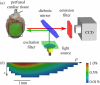
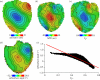
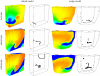
 estimated from optical action potentials at each pixel. (d) Subsurface angle, computed assuming transmural rotational anisotropy in the visualized geometry. (e) Relationship between subsurface angle and
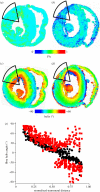
estimated from optical action potentials at each pixel. (d) Subsurface angle, computed assuming transmural rotational anisotropy in the visualized geometry. (e) Relationship between subsurface angle and  used for panel (d) and obtained using detailed photon migration models. Red line is the linear regression for steady-state wavefronts obtained using line excitation.
used for panel (d) and obtained using detailed photon migration models. Red line is the linear regression for steady-state wavefronts obtained using line excitation.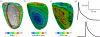

References
-
- Jalife J. 2000. Ventricular fibrillation: mechanisms of initiation and maintenance. Annu. Rev. Physiol. 62, 25–5010.1146/annurev.physiol.62.1.25 (doi:10.1146/annurev.physiol.62.1.25) - DOI - DOI - PubMed
-
- Vaquero M., Calvo D., Jalife J. 2008. Cardiac fibrillation: from ion channels to rotors in the human heart. Heart Rhythm 5, 872–87910.1016/j.hrthm.2008.02.034 (doi:10.1016/j.hrthm.2008.02.034) - DOI - DOI - PMC - PubMed
-
- Fenton F., Karma A. 1998. Vortex dynamics in three-dimensional continuous myocardium with fiber rotation: filament instability and fibrillation. Chaos 8, 20–4710.1063/1.166311 (doi:10.1063/1.166311) - DOI - DOI - PubMed
-
- Gray R. A., Pertsov A. M., Jalife J. 1998. Spatial and temporal organization during cardiac fibrillation. Nature 392, 75–7810.1038/32164 (doi:10.1038/32164) - DOI - DOI - PubMed
-
- Codreanu A., et al. 2008. Electroanatomic characterization of post-infarct scars: comparison with 3-dimensional myocardial scar reconstruction based on magnetic resonance imaging. J. Am. Coll. Cardiol. 52, 839–84210.1016/j.jacc.2008.05.038 (doi:10.1016/j.jacc.2008.05.038) - DOI - DOI - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources

