Statistical mechanics for natural flocks of birds
- PMID: 22427355
- PMCID: PMC3324025
- DOI: 10.1073/pnas.1118633109
Statistical mechanics for natural flocks of birds
Abstract
Flocking is a typical example of emergent collective behavior, where interactions between individuals produce collective patterns on the large scale. Here we show how a quantitative microscopic theory for directional ordering in a flock can be derived directly from field data. We construct the minimally structured (maximum entropy) model consistent with experimental correlations in large flocks of starlings. The maximum entropy model shows that local, pairwise interactions between birds are sufficient to correctly predict the propagation of order throughout entire flocks of starlings, with no free parameters. We also find that the number of interacting neighbors is independent of flock density, confirming that interactions are ruled by topological rather than metric distance. Finally, by comparing flocks of different sizes, the model correctly accounts for the observed scale invariance of long-range correlations among the fluctuations in flight direction.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

 .
.
 ) as a function of nc with J optimized for each value of nc; same snapshot as in A. There is a clear maximum at nc = 11. (Inset) the log-likelihood per bird for other snapshots of the same flocking event. (C) The inferred value of J for all observed flocks, shown as a function of the flock’s size. Each point corresponds to an average over all the snapshots of the same flock. Error bars are standard deviations across multiple snapshots. (D) As in C but for the inferred values of nc. Averaging over all flocks we find nc = 21.2 ± 1.7 (black line). (E) The inferred value of the topological range
) as a function of nc with J optimized for each value of nc; same snapshot as in A. There is a clear maximum at nc = 11. (Inset) the log-likelihood per bird for other snapshots of the same flocking event. (C) The inferred value of J for all observed flocks, shown as a function of the flock’s size. Each point corresponds to an average over all the snapshots of the same flock. Error bars are standard deviations across multiple snapshots. (D) As in C but for the inferred values of nc. Averaging over all flocks we find nc = 21.2 ± 1.7 (black line). (E) The inferred value of the topological range  as a function of the mean interbird distance in the flock, for all flocks. Error bars are standard deviations across multiple snapshots of the same flock. (F) As in E but for the metric range rc. If interactions extend over some fixed metric distance r0, then we expect
as a function of the mean interbird distance in the flock, for all flocks. Error bars are standard deviations across multiple snapshots of the same flock. (F) As in E but for the metric range rc. If interactions extend over some fixed metric distance r0, then we expect  and rc = constant; we find the opposite pattern, which is a signature of interactions with a fixed number of topological neighbors (14).
and rc = constant; we find the opposite pattern, which is a signature of interactions with a fixed number of topological neighbors (14).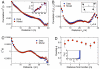
 . Because the two components have different amplitudes, it is convenient to look at them separately. (A) Perpendicular component of the correlation,
. Because the two components have different amplitudes, it is convenient to look at them separately. (A) Perpendicular component of the correlation,  , as a function of the distance; the average is performed over all pairs ij separated by distance r. Blue diamonds refer to experimental data (for the snapshot in Fig. 1), red circles to the prediction of the model in Eq. 4. The dashed line marks the maximum r that contributes to Cint, which is the only input to the model. The correlation function is well fitted over all length scales. In particular, the correlation length ξ, defined as the distance where the correlation crosses zero, is well reproduced by the model. (Inset) ξ vs. size of the flock, for all the flocking events; error bars are standard deviations across multiple snapshots of the same flocking event. (B) Four-point correlation function
, as a function of the distance; the average is performed over all pairs ij separated by distance r. Blue diamonds refer to experimental data (for the snapshot in Fig. 1), red circles to the prediction of the model in Eq. 4. The dashed line marks the maximum r that contributes to Cint, which is the only input to the model. The correlation function is well fitted over all length scales. In particular, the correlation length ξ, defined as the distance where the correlation crosses zero, is well reproduced by the model. (Inset) ξ vs. size of the flock, for all the flocking events; error bars are standard deviations across multiple snapshots of the same flocking event. (B) Four-point correlation function  , where the pairs ij and kl are as shown in the Inset (see also
, where the pairs ij and kl are as shown in the Inset (see also  , as a function of distance. Note that in the spin wave approximation, CL(r) = 1 - C4(0; r) - S2. (D) Similarity between the predicted mean value of flight direction,
, as a function of distance. Note that in the spin wave approximation, CL(r) = 1 - C4(0; r) - S2. (D) Similarity between the predicted mean value of flight direction,  , and real data, for all individual birds in the interior of the flock. The similarity can be quantified through the local overlap
, and real data, for all individual birds in the interior of the flock. The similarity can be quantified through the local overlap  , which is plotted as a function of the distance of the individual from the border. Maximal similarity corresponds to qi = 1. (Inset) Full distribution P(q) for all the interior birds.
, which is plotted as a function of the distance of the individual from the border. Maximal similarity corresponds to qi = 1. (Inset) Full distribution P(q) for all the interior birds.
References
-
- Camazine S, et al. Self-Organization in Biological Systems. Princeton: Princeton Univ Press; 2003.
-
- Anderson PW. More is different. Science. 1972;177:393–396. - PubMed
-
- Wilson KG. Problems in physics with many scales of length. Sci Am. 1979;241:158–179.
-
- Couzin ID, Krause J. Self-organization and collective behavior in vertebrates. Adv Study Behav. 2003;32:1–75.
-
- Binney J, Dowrick NJ, Fisher AJ, Newman MEJ. The Theory of Critical Phenomena. Oxford: Oxford Univ Press; 1992.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

