A network diffusion model of disease progression in dementia
- PMID: 22445347
- PMCID: PMC3623298
- DOI: 10.1016/j.neuron.2011.12.040
A network diffusion model of disease progression in dementia
Abstract
Patterns of dementia are known to fall into dissociated but dispersed brain networks, suggesting that the disease is transmitted along neuronal pathways rather than by proximity. This view is supported by neuropathological evidence for "prion-like" transsynaptic transmission of disease agents like misfolded tau and beta amyloid. We mathematically model this transmission by a diffusive mechanism mediated by the brain's connectivity network obtained from tractography of 14 healthy-brain MRIs. Subsequent graph theoretic analysis provides a fully quantitative, testable, predictive model of dementia. Specifically, we predict spatially distinct "persistent modes," which, we found, recapitulate known patterns of dementia and match recent reports of selectively vulnerable dissociated brain networks. Model predictions also closely match T1-weighted MRI volumetrics of 18 Alzheimer's and 18 frontotemporal dementia subjects. Prevalence rates predicted by the model strongly agree with published data. This work has many important implications, including dimensionality reduction, differential diagnosis, and especially prediction of future atrophy using baseline MRI morphometrics.
Copyright © 2012 Elsevier Inc. All rights reserved.
Figures

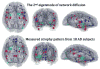
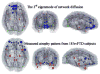





Comment in
-
Disintegrating brain networks: from syndromes to molecular nexopathies.Neuron. 2012 Mar 22;73(6):1060-2. doi: 10.1016/j.neuron.2012.03.006. Epub 2012 Mar 21. Neuron. 2012. PMID: 22445334 Free PMC article.
-
Neurodegenerative disease: Modelling connectivity networks of the brain--can neurodegeneration and dementia progression be predicted?Nat Rev Neurol. 2012 Apr 17;8(5):237. doi: 10.1038/nrneurol.2012.64. Nat Rev Neurol. 2012. PMID: 22508230 No abstract available.
-
Neurodegenerative networking.Nat Rev Neurosci. 2012 Apr 18;13(5):288. doi: 10.1038/nrn3248. Nat Rev Neurosci. 2012. PMID: 22510888 No abstract available.
References
-
- Acosta-Cabronero Julio, Williams Guy B, Pengas George, Nestor Peter J. Absolute diffusivities define the landscape of white matter degeneration in Alzheimer’s disease. Brain. 2010;133:529–539. - PubMed
-
- Alemán-Gómez Y, Melie-García L, Valdés-Hernandez P. IBASPM: toolbox for automatic parcellation of brain structures. Presented at the 12th Annual Meeting of the Organization for Human Brain Mapping; Florence, Italy. 2005.
-
- Almond DP, Budd CJ, McCullen NJ. Emergent behaviour in large electrical networks. In: Georgoulis E, Iske A, Levesley J, editors. Approximation Algorithms for Complex Systems. New York: Springer; 2011. pp. 3–26.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

