Dynamic effective connectivity of inter-areal brain circuits

Abstract

Anatomic connections between brain areas affect information flow between neuronal circuits and the synchronization of neuronal activity. However, such structural connectivity does not coincide with effective connectivity (or, more precisely, causal connectivity), related to the elusive question "Which areas cause the present activity of which others?". Effective connectivity is directed and depends flexibly on contexts and tasks. Here we show that dynamic effective connectivity can emerge from transitions in the collective organization of coherent neural activity. Integrating simulation and semi-analytic approaches, we study mesoscale network motifs of interacting cortical areas, modeled as large random networks of spiking neurons or as simple rate units. Through a causal analysis of time-series of model neural activity, we show that different dynamical states generated by a same structural connectivity motif correspond to distinct effective connectivity motifs. Such effective motifs can display a dominant directionality, due to spontaneous symmetry breaking and effective entrainment between local brain rhythms, although all connections in the considered structural motifs are reciprocal. We show then that transitions between effective connectivity configurations (like, for instance, reversal in the direction of inter-areal interactions) can be triggered reliably by brief perturbation inputs, properly timed with respect to an ongoing local oscillation, without the need for plastic synaptic changes. Finally, we analyze how the information encoded in spiking patterns of a local neuronal population is propagated across a fixed structural connectivity motif, demonstrating that changes in the active effective connectivity regulate both the efficiency and the directionality of information transfer. Previous studies stressed the role played by coherent oscillations in establishing efficient communication between distant areas. Going beyond these early proposals, we advance here that dynamic interactions between brain rhythms provide as well the basis for the self-organized control of this "communication-through-coherence", making thus possible a fast "on-demand" reconfiguration of global information routing modalities.

Figure 1. Flexibility of brain function requires dynamic effective connectivity.

This is illustrated by the example of a Giuseppe Arcimboldo's painting (Vertumnus; 1590, Skoklosters Slott, Sweden). A: the illusion of seeing a face is due to the default activation of a network of brain areas dedicated to face recognition. B: however, selective attention to individual components –e.g. to a pear or a flower– suppresses this illusion by modulating the interaction between these and other brain areas. Therefore, effective connectivity, i.e. the specific active pattern of inter-areal influences, needs to be rewired “on demand” in a fast and reliable way, without changes in the underlying structural connectivity between the involved areas.

Figure 2. Models of interacting areas.

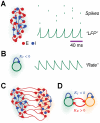
A: in the network model, each local area is modeled as a large network of randomly and sparsely interconnected excitatory and inhibitory spiking neurons (inhibitory cells and synapses are in blue, excitatory cells and synapses are in red, ). Individual neurons spike irregularly (see the spike trains of eight representative neurons, top right), but the activity of the network undergoes a collective fast oscillation, visible in the average membrane potential (see example “LFP” trace, bottom right). B: in the rate model, each local area is modeled by a single mean-field rate unit with delayed local inhibition (of strength ). Its dynamics, describing the average area activity, also undergoes a fast oscillation (see example rate trace, right). C–D: the interaction between multiple local areas ( in the case of the reported graphical illustrations, green and orange shading indicate separate areas) is modeled by the dynamics: of multiple local spiking networks, mutually interconnected by long-range excitatory synapses (see panel C); or of multiple rate units, coupled reciprocally by delayed excitation (of strength , see panel D).

Figure 3. Effective motifs of the unidirectional driving family.

For weak inter-areal coupling strengths, out-of-phase lockings of local periodic oscillations give rise to a family of “unidirectional driving” effective motif. The figure shows dynamics and corresponding effective connectivities for fully symmetric structural motifs with (panels A–B) or (panels C–D) areas. A: the dynamics of interacting areas (green and orange colors) is illustrated by “LFPs” (left, top row) and representative spike trains (left, middle row, two cells per each area) from the network model (horizontal bar is , vertical bar is ), as well as by matching rate traces (left, bottom row) from the rate model (arbitrary time units). The right sub-panel reports the associated effective connectivity measured by Transfer Entropy (TE), evaluated from “LFPs” time-series, for all possible directed interactions (indicated by colored arrows). Boxes indicate the interquartile range and whiskers the confidence interval for the estimated TEs. TEs above the grey horizontal band indicate statistically significant causal influences (see Methods ). B: to the right of the corresponding box-plot, effective connectivity is also represented in a diagrammatic form. Arrow thicknesses encode the strength of corresponding causal interactions (if statistically significant). Below this effective motif, a second motif in the same unidirectional driving family is plotted (with a smaller size), corresponding to another motif version with equivalent overall topology but reversed directionality. The parameters used for are, for the network model: , ; and for the rate model: , , . C: this panels reports similar quantities as panel A, but now for a structural motif with areas (green, orange and light blue colors). Effective connectivity is now measured by partialized Transfer Entropy (pTE; see Methods ), in order to account only for direct causal interactions. D: the six effective motifs of the unidirectional driving family for are also reported. The parameters used for are, for the network model: , ; and for the rate model: , , .

Figure 4. Effective motifs of the leaky driving family.

The figure shows dynamics and corresponding effective connectivities for fully symmetric structural motifs with (panels A–B) or (panels C–D) areas, for intermediate inter-areal coupling strength, leading to asymmetrically irregular oscillations, phase-locked with an average out-of-phase relation. A: the dynamics of interacting areas (green and orange colors) is illustrated by “LFPs” (left, top row) and representative spike trains (left, middle row, two cells per each area) from the network model (horizontal bar is , vertical bar is ), as well as by matching rate traces (left, bottom row) from the rate model (arbitrary time units). The right sub-panel reports the associated effective connectivity measured by Transfer Entropy (TE), evaluated from “LFPs” time-series, for all possible directed interactions (indicated by colored arrows). Boxes indicate the interquartile range and whiskers the confidence interval for the estimated TEs. TEs above the grey horizontal band indicate statistically significant causal influences (see Methods ). B: to the right of the corresponding box-plot, effective connectivity is also represented in a diagrammatic form. Arrow thicknesses encode the strength of corresponding causal interactions (if statistically significant). Below this effective motif, a second motif in the same unidirectional driving family is plotted (with a smaller size), corresponding to another motif version with equivalent overall topology but reversed directionality. The parameters used for are, for the network model: , ; and for the rate model: , , . C: this panels reports similar quantities as panel A, but now for a structural motif with areas (green, orange and light blue colors). Effective connectivity is measured by partialized Transfer Entropy (pTE; see Methods ), in order to account for direct but not for indirect causal interactions. D: the six effective motifs of the unidirectional driving family for are also reported. The parameters used for are, for the network model: , ; and for the rate model: , , .

Figure 5. Effective motifs of the mutual driving family.

The figure shows dynamics and corresponding effective connectivities for fully symmetric structural motifs with (panels A–B) or (panels C–D) areas, for large inter-areal coupling strength, leading to symmetrically irregular oscillations, without a stable phase relation. A: the dynamics of interacting areas (green and orange colors) is illustrated by “LFPs” (left, top row) and representative spike trains (left, middle row, two cells per each area) from the network model (horizontal bar is , vertical bar is ), as well as by matching rate traces (left, bottom row) from the rate model (arbitrary time units). The right sub-panel reports the associated effective connectivity measured by Transfer Entropy (TE), evaluated from “LFPs” time-series, for all possible directed interactions (indicated by colored arrows). Boxes indicate the interquartile range and whiskers the confidence interval for the estimated TEs. TEs above the grey horizontal band indicate statistically significant causal influences (see Methods ). B: to the right of the corresponding box-plot, effective connectivity is also represented in a diagrammatic form. Arrow thicknesses encode the strength of corresponding causal interactions (if statistically significant). A single motif is included in this family The parameters used for are, for the network model: , ; and for the rate model: , , . C: this panels reports similar quantities as panel A, but now for a structural motif with areas (green, orange and light blue colors). Effective connectivity is measured by partialized Transfer Entropy (pTE; see Methods ), in order to account for direct but not for indirect causal interactions. D: the mutual driving effective motif for is also reported. The parameters used for are, for the network model: , ; and for the rate model: , , .

Figure 6. Dynamic control of effective connectivity.

A: symmetric structural motifs can give rise to asymmetric dynamics in which one area leads in phase over the other (spontaneous symmetry breaking). Basins of attraction (in phase-shift space) of distinct phase-locking configurations are schematically shown here (for ). Empty circles stand for unstable in- and anti-phase lockings and filled circles for stable out-of-phase lockings (corresponding to unidirectional driving effective motifs). B: phase-shift evolution function for the rate model (left, analytical solution, ) and for the network model (right, numerical evaluation, ). Empty and filled circles denote the same stable and unstable phase-lockings as in panel A. C: cartoon of successful (dashed green arrow) and unsuccessful (dashed grey arrow) switchings induced by brief perturbations (lightning icon). An input pulse to the system destabilizes transiently the current phase-locking (solid red and green arrows). For most perturbations, the system does not leave the current basin of attraction and the previous effective motif is restored (dashed red arrow). However, suitable perturbations can lead the system to switch to a different effective motif (dashed green arrow). D: a pulse of strength induces a phase advancement of the collective oscillations, depending on its application phase , as described by the Phase Response Curve (left, rate model; analytical solution, ) or by the induced shift (right, network model; numerical evaluation, ). E–F: frequency histogram of successful switching for pulses applied at different phases (the laggard area is perturbed; for the rate model and for the network model). Predicted intervals for successful switching are marked in green, for the unidirectional (panel E) and for the leaky effective driving (panel F) motifs (left, rate model; right, network model; parameters as in Figures 3 and 4). Diagrams of the induced transitions are shown in the third column (see SI, Figure S2 for perturbations applied to the leader area).

Figure 7. Effective entrainment.

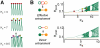
A: examples of rate oscillations for different values of the inter-areal coupling in the rate model (, , from bottom to top). Filled circles denote peaks of oscillation cycles, different color fillings denote different peak amplitudes. B: The oscillatory dynamics is qualitatively altered by increasing inter-areal coupling, as visualized by bifurcation diagrams, constructed by plotting different peak amplitudes at constant , as different dots (the dots corresponding to the peak amplitudes in panel A, are highlighted also here by filled circles of matching colors). Varying in a continuous range, these dots trace a complex branched structure, denoting emergence of novel dynamical states. The bifurcation diagrams for the case of two symmetrically connected areas (top) and two unidirectionally connected areas (bottom) are very similar. For a symmetric structural motif, spontaneous symmetry breaking leads to effective entrainment, mimicking the direct entrainment, which occurs for an asymmetric unidirectional structural motif. Leader and laggard areas in effective entrainment behave similarly to the driver and driven area in direct entrainment (orange and green bifurcation diagrams, respectively). Note that different structural motifs give rise to equivalent effective motifs (see side diagrams). Note: a different version of panel B was previously published in as Supplementary Figure F.

Figure 8. Effective connectivity affects information propagation.

A: in the case of sparsely synchronized oscillations, individual neurons fire irregularly (see four example spike trains, middle row) even when the local area activity undergoes a very regular collective rhythm (evident in “LFP” traces, bottom row). Therefore, a large amount of information can be potentially encoded, at every (analog) oscillation cycle, in the form of (digital-like) codewords in which “1” or “0” entries denote respectively firing or missed firing of a specific neuron in the considered cycle (top row). B: the strength of specific subsets of long-range excitatory synapses is systematically enhanced in order to form unidirectional “transmission lines” (TLs) embedded into the symmetric structural motif (see Methods ). Cells and synapses belonging to TLs are highlighted by pale green (“green-to-orange” area direction) and lilac (“orange-to-green” area direction) colors. Communication efficiency along TLs is quantified by the Mutual Information () between spike trains of pairs of source and target cells connected directly by a TL synapse, normalized by the entropy () of the source cell. C–D: boxplots (see Figures 3, 4 and 5) of for different groups of interconnected cells and for different active effective motifs. Pale green and lilac arrows below the boxplots indicate pairs of cells interconnected by the TL marked with the corresponding color. A dot indicates control pairs of cells interconnected by ordinary weak long-range synapses. Green and orange arrows indicate the dominant directionality of the active effective connectivity motif. C: unidirectional driving effective motif family. Communication efficiency is enhanced only along the TL aligned to the directionality of the active effective connectivity, while it is undistinguishable from control along the other TL. D: leaky driving effective motif family. Communication efficiency is enhanced along both TLs, but more along the TL aligned to the dominant directionality of the active effective connectivity.

Figure 9. Transfer entropy depends on time lag and quantization.

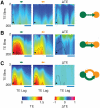
A–C: The matrices in these panels illustrate the dependence of TE (network model, fully symmetric structural motif, cfr. Figures 3, 4 and 5) on the number of discretization bins used to describe the time-series of neural activity and on the adopted time lag between the time-series (see Methods ). The matrices in the first two columns (from the left) report TEs in the two possible interaction directions, and , and the matrices in the third column visualize the causal unbalancing (), which quantifies the asymmetry between causal influences in the two directions (see Methods ). All of these quantities are evaluated for different combinations of and . The vertical axes of the matrices correspond to the range bins and the horizontal axes to the range . This range of time lags corresponds approximately to three oscillation periods. Horizontal scale lines indicate the average oscillation period (, respectively for panels A, B and C). Values of TE and are color-coded (see color bars at the bottom, note the two different color scales for TE and ). Black dotted lines in the matrices enclose regions in which or rise above the threshold for significancy of the corresponding causal interaction (see Methods ). These significance contours are overlayed in the corresponding matrix. A star denotes the combination of and used for the analysis throughout the main article (, ). Different rows report TE matrices for different effective motifs. A: unidirectional driving effective motif. B: leaky driving effective motif. C: mutual driving effective motif. Diagrams of these effective motifs are drawn in the fourth column as a visual reference. All other parameters are as for the analyses of Figures 3, 4 and 5.