Hierarchy measure for complex networks
- PMID: 22470477
- PMCID: PMC3314676
- DOI: 10.1371/journal.pone.0033799
Hierarchy measure for complex networks
Abstract
Nature, technology and society are full of complexity arising from the intricate web of the interactions among the units of the related systems (e.g., proteins, computers, people). Consequently, one of the most successful recent approaches to capturing the fundamental features of the structure and dynamics of complex systems has been the investigation of the networks associated with the above units (nodes) together with their relations (edges). Most complex systems have an inherently hierarchical organization and, correspondingly, the networks behind them also exhibit hierarchical features. Indeed, several papers have been devoted to describing this essential aspect of networks, however, without resulting in a widely accepted, converging concept concerning the quantitative characterization of the level of their hierarchy. Here we develop an approach and propose a quantity (measure) which is simple enough to be widely applicable, reveals a number of universal features of the organization of real-world networks and, as we demonstrate, is capable of capturing the essential features of the structure and the degree of hierarchy in a complex network. The measure we introduce is based on a generalization of the m-reach centrality, which we first extend to directed/partially directed graphs. Then, we define the global reaching centrality (GRC), which is the difference between the maximum and the average value of the generalized reach centralities over the network. We investigate the behavior of the GRC considering both a synthetic model with an adjustable level of hierarchy and real networks. Results for real networks show that our hierarchy measure is related to the controllability of the given system. We also propose a visualization procedure for large complex networks that can be used to obtain an overall qualitative picture about the nature of their hierarchical structure.
Conflict of interest statement
Figures
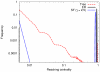
 parameter values. Each distribution is averaged over 1000 AH networks with
parameter values. Each distribution is averaged over 1000 AH networks with  and
and  . The standard deviations of the distributions are comparable to the averages only for relative frequencies less than 0.002. Note that from the
. The standard deviations of the distributions are comparable to the averages only for relative frequencies less than 0.002. Note that from the  (highly random) to the
(highly random) to the  (fully hierarchical) state the distribution changes continuously and monotonously with
(fully hierarchical) state the distribution changes continuously and monotonously with  .
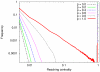
.
 and different average degrees. Standard deviations grow with
and different average degrees. Standard deviations grow with  , but they are clearly below the average values of the GRC. Note that for larger density, it is less likely to obtain the same level of hierarchy.
, but they are clearly below the average values of the GRC. Note that for larger density, it is less likely to obtain the same level of hierarchy.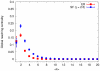
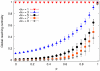
 nodes. In the Erdös–Rényi and scale-free networks, standard deviations of the GRC are comparable with its averages only for
nodes. In the Erdös–Rényi and scale-free networks, standard deviations of the GRC are comparable with its averages only for  and
and  , respectively.
, respectively.
 nodes and the ER and SF graphs have
nodes and the ER and SF graphs have  . In each network
. In each network  was set to
was set to  .
.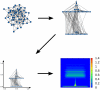
 local quantity for each graph in the ensemble (top right). Next, we separate the levels logarithmically and scale each layout into the unit square (bottom left). Last, we overlay all rescaled layouts and plot the obtained density of nodes in the unit square (bottom right, see color scale also). In the heat maps, the color scale shows
local quantity for each graph in the ensemble (top right). Next, we separate the levels logarithmically and scale each layout into the unit square (bottom left). Last, we overlay all rescaled layouts and plot the obtained density of nodes in the unit square (bottom right, see color scale also). In the heat maps, the color scale shows  , where
, where  is the average density of the ensemble.
is the average density of the ensemble.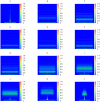
 ). In each case the color scale shows
). In each case the color scale shows  where
where  is the density averaged over 1000 graphs.
is the density averaged over 1000 graphs.  and
and  were set. In every network,
were set. In every network,  was set to
was set to  . The corresponding GRC values are: 0.997 (A), 0.058 (B), 0.127 (C), 0.135 (D), 0.161 (E), 0.194 (F), 0.238 (G), 0.290 (H), 0.361 (I), 0.452 (J), 0.581 (K) and 0.775 (L).
. The corresponding GRC values are: 0.997 (A), 0.058 (B), 0.127 (C), 0.135 (D), 0.161 (E), 0.194 (F), 0.238 (G), 0.290 (H), 0.361 (I), 0.452 (J), 0.581 (K) and 0.775 (L).
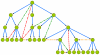
 was set to
was set to  .
.
 and for the Erdös–Rényi (ER) and scale-free (SF) networks
and for the Erdös–Rényi (ER) and scale-free (SF) networks  . All curves show averages of the distributions over an ensemble of 1000 graphs. Standard deviations are comparable with the averages only near the peaks in the ER and SF models. Although the standard deviations at the peaks are large, they do not change the positions of the peaks, and thus, do not affect the distributions.
. All curves show averages of the distributions over an ensemble of 1000 graphs. Standard deviations are comparable with the averages only near the peaks in the ER and SF models. Although the standard deviations at the peaks are large, they do not change the positions of the peaks, and thus, do not affect the distributions.References
-
- Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Phys Rev Lett. 2009;81:591–646.
-
- Vicsek T, Zafiris A. Collective motion. 2010. arxiv:1010.5017.
-
- Pastor-Satorras R, Vespignani A. Evolution and Strcuture of the Internet. Cambridge: Cambridge University Press; 2004.
-
- Albert R, Barabási AL. Statistical Mechanics of Complex Networks. Phys Rev Lett. 2002;74:47–97.
-
- Pumain D, editor. Hierarchy in Natural and Social Sciences. Dodrecht, The Netherlands: Springer; 2006. pp. 1–12.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

