Physical constraints on charge transport through bacterial nanowires
- PMID: 22470966
- PMCID: PMC3392031
- DOI: 10.1039/c1fd00098e
Physical constraints on charge transport through bacterial nanowires
Abstract
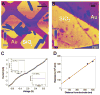
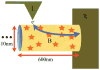
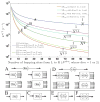
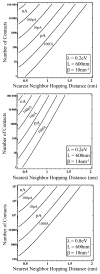
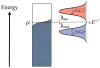
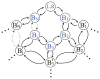
Extracellular appendages of the dissimilatory metal-reducing bacterium Shewanella oneidensis MR-1 were recently shown to sustain currents of 10(10) electrons per second over distances of 0.5 microns [El-Naggar et al., Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 18127]. However, the identity of the charge localizing sites and their organization along the "nanowire" remain unknown. We use theory to predict redox cofactor separation distances that would permit charge flow at rates of 10(10) electrons per second over 0.5 microns for voltage biases of < or = IV, using a steady-state analysis governed by a non-adiabatic electron transport mechanism. We find the observed currents necessitate a multi-step hopping transport mechanism, with charge localizing sites separated by less than 1 nm and reorganization energies that rival the lowest known in biology.
Figures


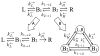
References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

