Structural diversity in social contagion
- PMID: 22474360
- PMCID: PMC3341012
- DOI: 10.1073/pnas.1116502109
Structural diversity in social contagion
Abstract
The concept of contagion has steadily expanded from its original grounding in epidemic disease to describe a vast array of processes that spread across networks, notably social phenomena such as fads, political opinions, the adoption of new technologies, and financial decisions. Traditional models of social contagion have been based on physical analogies with biological contagion, in which the probability that an individual is affected by the contagion grows monotonically with the size of his or her "contact neighborhood"--the number of affected individuals with whom he or she is in contact. Whereas this contact neighborhood hypothesis has formed the underpinning of essentially all current models, it has been challenging to evaluate it due to the difficulty in obtaining detailed data on individual network neighborhoods during the course of a large-scale contagion process. Here we study this question by analyzing the growth of Facebook, a rare example of a social process with genuinely global adoption. We find that the probability of contagion is tightly controlled by the number of connected components in an individual's contact neighborhood, rather than by the actual size of the neighborhood. Surprisingly, once this "structural diversity" is controlled for, the size of the contact neighborhood is in fact generally a negative predictor of contagion. More broadly, our analysis shows how data at the size and resolution of the Facebook network make possible the identification of subtle structural signals that go undetected at smaller scales yet hold pivotal predictive roles for the outcomes of social processes.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
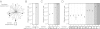
 confidence intervals and implicitly reveal the relative frequency of the different topologies.
confidence intervals and implicitly reveal the relative frequency of the different topologies.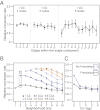
 confidence intervals.
confidence intervals.
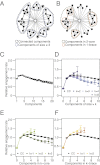
 . (B) Illustration of the k-core and the k-brace, delineating the connected components of the 2-core and the 1-brace. (C) Engagement as a function of connected component count. (D) Engagement as a function of the number of components of size
. (B) Illustration of the k-core and the k-brace, delineating the connected components of the 2-core and the 1-brace. (C) Engagement as a function of connected component count. (D) Engagement as a function of the number of components of size  , for
, for  , with connected component (CC) count shown for comparison. (E) Engagement as a function of k-core component count for
, with connected component (CC) count shown for comparison. (E) Engagement as a function of k-core component count for  , with CC count shown for comparison. (F) Engagement as a function of k-brace component count for
, with CC count shown for comparison. (F) Engagement as a function of k-brace component count for  , with CC count shown for comparison. Engagement rates are reported on a relative scale, where 1.0 signifies the average conversion rate of all 50-node neighborhoods. All error bars are 95% confidence intervals. For other neighborhood sizes, see
, with CC count shown for comparison. Engagement rates are reported on a relative scale, where 1.0 signifies the average conversion rate of all 50-node neighborhoods. All error bars are 95% confidence intervals. For other neighborhood sizes, see 
 , we see that when component count is not accounted for, an internal engagement optimum is observed, showing the combined forces of focused context and structural heterogeneity. Engagement rates are reported on a relative scale, where 1.0 signifies the average conversion rate of all 50-node neighborhoods. All error bars are 95% confidence intervals.
, we see that when component count is not accounted for, an internal engagement optimum is observed, showing the combined forces of focused context and structural heterogeneity. Engagement rates are reported on a relative scale, where 1.0 signifies the average conversion rate of all 50-node neighborhoods. All error bars are 95% confidence intervals.Similar articles
-
Locating privileged spreaders on an online social network.Phys Rev E Stat Nonlin Soft Matter Phys. 2012 Jun;85(6 Pt 2):066123. doi: 10.1103/PhysRevE.85.066123. Epub 2012 Jun 19. Phys Rev E Stat Nonlin Soft Matter Phys. 2012. PMID: 23005178
-
Modeling Contagion Through Social Networks to Explain and Predict Gunshot Violence in Chicago, 2006 to 2014.JAMA Intern Med. 2017 Mar 1;177(3):326-333. doi: 10.1001/jamainternmed.2016.8245. JAMA Intern Med. 2017. PMID: 28055070
-
Multi-stage complex contagions.Chaos. 2013 Mar;23(1):013124. doi: 10.1063/1.4790836. Chaos. 2013. PMID: 23556961
-
Contagion: a theoretical and empirical review and reconceptualization.Genet Soc Gen Psychol Monogr. 1993 May;119(2):233-84. Genet Soc Gen Psychol Monogr. 1993. PMID: 8405969 Review.
-
Broadening the Perspective on Emotional Contagion and Emotional Mimicry: The Correction Hypothesis.Perspect Psychol Sci. 2019 May;14(3):437-451. doi: 10.1177/1745691618808523. Epub 2019 Mar 7. Perspect Psychol Sci. 2019. PMID: 30844340 Review.
Cited by
-
Uncertainty analysis of contagion processes based on a functional approach.Sci Rep. 2023 Sep 19;13(1):15522. doi: 10.1038/s41598-023-42041-0. Sci Rep. 2023. PMID: 37726315 Free PMC article.
-
Profiling the best-performing community medicine distributors for mass drug administration: a comprehensive, data-driven analysis of treatment for schistosomiasis, lymphatic filariasis, and soil-transmitted helminths in Uganda.BMC Med. 2019 Mar 28;17(1):69. doi: 10.1186/s12916-019-1303-z. BMC Med. 2019. PMID: 30917824 Free PMC article.
-
Cumulative effect in information diffusion: empirical study on a microblogging network.PLoS One. 2013 Oct 1;8(10):e76027. doi: 10.1371/journal.pone.0076027. eCollection 2013. PLoS One. 2013. PMID: 24098422 Free PMC article.
-
An improved local immunization strategy for scale-free networks with a high degree of clustering.Eur Phys J B. 2017;90(1):2. doi: 10.1140/epjb/e2016-70334-9. Epub 2017 Jan 11. Eur Phys J B. 2017. PMID: 32214893 Free PMC article.
-
Evolution characteristics of the network core in the Facebook.PLoS One. 2014 Aug 28;9(8):e104028. doi: 10.1371/journal.pone.0104028. eCollection 2014. PLoS One. 2014. PMID: 25165852 Free PMC article.
References
-
- Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks. Phys Rev Lett. 2001;86:3200–3203. - PubMed
-
- Dodds PS, Watts DJ. Universal behavior in a generalized model of contagion. Phys Rev Lett. 2004;92:218701. - PubMed
-
- Backstrom L, Huttenlocher D, Kleinberg J, Lan X. Group formation in large social networks: Membership, growth, and evolution. In: Eliassi-Rad T, Ungar LH, Craven M, Gunopulos D, editors. Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: Association for Computing Machinery; 2006. pp. 44–54.
-
- Kearns M, Suri S, Montfort N. An experimental study of the coloring problem on human subject networks. Science. 2006;313:824–827. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

