Fragmentation: loss of global coherence or breakdown of modularity in functional brain architecture?

Abstract

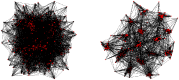
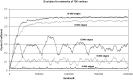
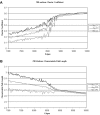
Psychiatric illnesses characterized by disorganized cognition, such as schizophrenia, have been described in terms of fragmentation and hence understood as reduction in functional brain connectivity, particularly in prefrontal and parietal areas. However, as graph theory shows, relatively small numbers of nonlocal connections are sufficient to ensure global coherence in the modular small-world network structure of the brain. We reconsider fragmentation in this perspective. Computational studies have shown that for a given level of connectivity in a model of coupled nonlinear oscillators, modular small-world networks evolve from an initially random organization. Here we demonstrate that with decreasing connectivity, the probability of evolving into a modular small-world network breaks down at a critical point, which scales to the percolation function of random networks with a universal exponent of α = 1.17. Thus, according to the model, local modularity systematically breaks down before there is loss of global coherence in network connectivity. We, therefore, propose that fragmentation may involve, at least in its initial stages, the inability of a dynamically evolving network to sustain a modular small-world structure. The result is in a shift in the balance in schizophrenia from local to global functional connectivity.

Keywords: complex system; computer simulation; connectivity; percolation; schizophrenia; small-world.

Figure 1

Adaptive rewiring leads from an initial random network (left), to modular small-world structure (right) in small iterative steps. Coupled chaotic oscillators intermittently synchronize and desynchronize their activity spontaneously in patterns of great variability. After some time a momentarily synchronized pair of units that are not connected receive a connection, which is removed from a pair that are connected but not synchronized. As this process continues, a modular, small-world structure emerges from an initially random configuration. To obtain a more detailed view of this phase transition, we use the adaptive rewiring scenario with coupled nonlinear maps (Kaneko, 1989) with initially randomly structured graphs, for a range of different numbers of vertices v: v = 300, 400, 500,…,1000 vertices and numbers of edges E that differ by small steps of 20. For each combination of v, E, across four million iterations we measured the CC and the CPL every one thousand iterations, resulting in a 4000 point record for each of five runs. The maximum, minimum, and mean values of the last 2000 points in each run were averaged over the five runs as illustrated in Figure 3.

Figure 2

Self-organization from random to small-world critically in a network of 700 vertices. The self-organization occurs through adaptive rewiring. Whether a small-world emerges depends on the number of edges.

Figure 3

Evolution under adaptive rewiring of maximum, minimum, and average cluster coefficient and characteristic path length. (A) The values of minimum, maximum and average CC for networks of 700 vertices and edges ranging from [7000, 7020, 7040,…,10,000] after extensive adaptive rewiring. Note that beyond 9000 edges, CC-values tighten to a narrow range, indicating strong and consistent clustering behavior. (B) The values of minimum, maximum, and average CPL for networks of 700 vertices and edges ranging from [7000, 7020, 7040,…,10,000] after extensive adaptive rewiring. Beyond 9000 edges, CPL-values also tighten to a narrow range of low values. Thus, for 700 vertices, at least 9000 edges are needed for adaptive rewiring to converge to small-world structure.

Figure 4

Universal scaling in the clustering threshold for self-organized small-world networks. Gray lines represent minimal, maximal and average observed values for clustering coefficient, the dotted line is the predicted clustering coefficient, CCpred, a linear function of the percolation function Cp(n) of a random graph of n vertices: CCpred = k₃ + k₄ × Cp(n) fitted with parameters k₃ and k₄ to the minimum observed clustering; the arrow indicates its anchor point ASWN(n) with the corresponding number of edges in parentheses.