Event timing in associative learning: from biochemical reaction dynamics to behavioural observations
- PMID: 22493657
- PMCID: PMC3316544
- DOI: 10.1371/journal.pone.0032885
Event timing in associative learning: from biochemical reaction dynamics to behavioural observations
Abstract
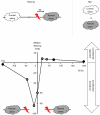
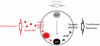
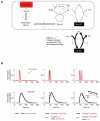
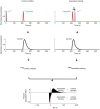
Associative learning relies on event timing. Fruit flies for example, once trained with an odour that precedes electric shock, subsequently avoid this odour (punishment learning); if, on the other hand the odour follows the shock during training, it is approached later on (relief learning). During training, an odour-induced Ca(++) signal and a shock-induced dopaminergic signal converge in the Kenyon cells, synergistically activating a Ca(++)-calmodulin-sensitive adenylate cyclase, which likely leads to the synaptic plasticity underlying the conditioned avoidance of the odour. In Aplysia, the effect of serotonin on the corresponding adenylate cyclase is bi-directionally modulated by Ca(++), depending on the relative timing of the two inputs. Using a computational approach, we quantitatively explore this biochemical property of the adenylate cyclase and show that it can generate the effect of event timing on associative learning. We overcome the shortage of behavioural data in Aplysia and biochemical data in Drosophila by combining findings from both systems.
Conflict of interest statement
Figures

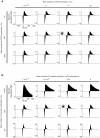
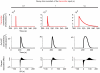
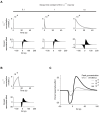

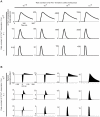
Similar articles
-
Biochemical studies of stimulus convergence during classical conditioning in Aplysia: dual regulation of adenylate cyclase by Ca2+/calmodulin and transmitter.J Neurosci. 1991 Sep;11(9):2655-65. doi: 10.1523/JNEUROSCI.11-09-02655.1991. J Neurosci. 1991. PMID: 1679120 Free PMC article.
-
A quantitative study of the Ca2+/calmodulin sensitivity of adenylyl cyclase in Aplysia, Drosophila, and rat.J Neurochem. 1992 Nov;59(5):1736-44. doi: 10.1111/j.1471-4159.1992.tb11005.x. J Neurochem. 1992. PMID: 1402918
-
Biochemical correlates of short-term sensitization in Aplysia: temporal analysis of adenylate cyclase stimulation in a perfused-membrane preparation.Proc Natl Acad Sci U S A. 1987 Dec;84(24):9285-9. doi: 10.1073/pnas.84.24.9285. Proc Natl Acad Sci U S A. 1987. PMID: 2892199 Free PMC article.
-
The biochemistry of learning and memory.Mol Cell Biochem. 1995 Aug-Sep;149-150:279-86. doi: 10.1007/BF01076589. Mol Cell Biochem. 1995. PMID: 8569741 Review.
-
The regulatory diversity of the mammalian adenylyl cyclases.Curr Opin Cell Biol. 1993 Apr;5(2):269-73. doi: 10.1016/0955-0674(93)90115-7. Curr Opin Cell Biol. 1993. PMID: 8507499 Review.
Cited by
-
Predictive olfactory learning in Drosophila.Sci Rep. 2021 Mar 24;11(1):6795. doi: 10.1038/s41598-021-85841-y. Sci Rep. 2021. PMID: 33762640 Free PMC article.
-
Signaling models for dopamine-dependent temporal contiguity in striatal synaptic plasticity.PLoS Comput Biol. 2020 Jul 23;16(7):e1008078. doi: 10.1371/journal.pcbi.1008078. eCollection 2020 Jul. PLoS Comput Biol. 2020. PMID: 32701987 Free PMC article.
-
Local 5-HT signaling bi-directionally regulates the coincidence time window for associative learning.Neuron. 2023 Apr 5;111(7):1118-1135.e5. doi: 10.1016/j.neuron.2022.12.034. Epub 2023 Jan 26. Neuron. 2023. PMID: 36706757 Free PMC article.
-
The critical balance between dopamine D2 receptor and RGS for the sensitive detection of a transient decay in dopamine signal.PLoS Comput Biol. 2021 Sep 30;17(9):e1009364. doi: 10.1371/journal.pcbi.1009364. eCollection 2021 Sep. PLoS Comput Biol. 2021. PMID: 34591840 Free PMC article.
-
Dopaminergic neurons write and update memories with cell-type-specific rules.Elife. 2016 Jul 21;5:e16135. doi: 10.7554/eLife.16135. Elife. 2016. PMID: 27441388 Free PMC article.
References
-
- Rescorla RA. Behavioral studies of Pavlovian conditioning. Annu Rev Neurosci. 1988;11:329–352. - PubMed
-
- Solomon RL, Corbit JD. An opponent-process theory of motivation. I. Temporal dynamics of affect. Psychol Rev. 1974;81:119–145. - PubMed
-
- Wagner AR. SOP: A model of automatic memory processing in animal behavior. In: Spear NE, Miller RR, editors. Information Processing in Animals: Memory Mechanisms. Hillsdale, NJ: Erlbaum; 1981. pp. 5–47.
-
- Sutton RS, Barto AG. Time-derivative models of pavlovian reinforcement. In: Gabriel M, Moore J, editors. Learning and computational neuroscience: Foundations of adaptive networks. Cambridge, MA: MIT Press; 1990. pp. 497–537.
-
- Chang RC, Blaisdell AP, Miller RR. Backward conditioning: mediation by the context. J Exp Psychol Anim Behav Process. 2003;29:171–183. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

