How to make epidemiological training infectious
- PMID: 22509129
- PMCID: PMC3317897
- DOI: 10.1371/journal.pbio.1001295
How to make epidemiological training infectious
Abstract
Modern infectious disease epidemiology builds on two independently developed fields: classical epidemiology and dynamical epidemiology. Over the past decade, integration of the two fields has increased in research practice, but training options within the fields remain distinct with few opportunities for integration in the classroom. The annual Clinic on the Meaningful Modeling of Epidemiological Data (MMED) at the African Institute for Mathematical Sciences has begun to address this gap. MMED offers participants exposure to a broad range of concepts and techniques from both epidemiological traditions. During MMED 2010 we developed a pedagogical approach that bridges the traditional distinction between classical and dynamical epidemiology and can be used at multiple educational levels, from high school to graduate level courses. The approach is hands-on, consisting of a real-time simulation of a stochastic outbreak in course participants, including realistic data reporting, followed by a variety of mathematical and statistical analyses, stemming from both epidemiological traditions. During the exercise, dynamical epidemiologists developed empirical skills such as study design and learned concepts of bias while classical epidemiologists were trained in systems thinking and began to understand epidemics as dynamic nonlinear processes. We believe this type of integrated educational tool will prove extremely valuable in the training of future infectious disease epidemiologists. We also believe that such interdisciplinary training will be critical for local capacity building in analytical epidemiology as Africa continues to produce new cohorts of well-trained mathematicians, statisticians, and scientists. And because the lessons draw on skills and concepts from many fields in biology--from pathogen biology, evolutionary dynamics of host--pathogen interactions, and the ecology of infectious disease to bioinformatics, computational biology, and statistics--this exercise can be incorporated into a broad array of life sciences courses.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
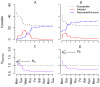
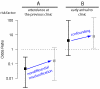
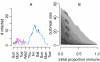
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

