The limits to parapatric speciation: Dobzhansky-Muller incompatibilities in a continent-island model

Abstract

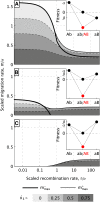
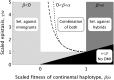
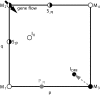
How much gene flow is needed to inhibit speciation by the accumulation of Dobzhansky-Muller incompatibilities (DMIs) in a structured population? Here, we derive these limits in a classical migration-selection model with two haploid or diploid loci and unidirectional gene flow from a continent to an island. We discuss the dependence of the maximum gene-flow rate on ecological factors (exogeneous selection), genetic factors (epistasis, recombination), and the evolutionary history. Extensive analytical and numerical results show the following: (1) The maximum rate of gene flow is limited by exogeneous selection. In particular, maintenance of neutral DMIs is impossible with gene flow. (2) There are two distinct mechanisms that drive DMI evolution in parapatry, selection against immigrants in a heterogeneous environment and selection against hybrids due to the incompatibility. (3) Depending on the mechanism, opposite predictions result concerning the genetic architecture that maximizes the rate of gene flow a DMI can sustain. Selection against immigrants favors evolution of tightly linked DMIs of arbitrary strength, whereas selection against hybrids promotes the evolution of strong unlinked DMIs. In diploids, the fitness of the double heterozygotes is the decisive factor to predict the pattern of DMI stability.

Figure 1

Maximum migration rates (black solid lines) and degree of population differentiation (gray areas) as functions of the (scaled) recombination rate r. We identify three regimes. (A) Selection against immigrants for slope-type fitness. Here, β/α = −0.6, γ/α = 2.5. (C) Selection against hybrids in a homogeneous environment. Here, β/α = 1.2, γ/α = 4. (B) Combination of both for intermediate fitness combinations. Here, β/α = 0.6, γ/α = 4. The corresponding type of fitness landscapes is displayed in each respective top right corner.

Figure 2

Parameter ranges corresponding to two different mechanisms for DMI evolution in the haploid model as a function of the heterogeneity of the environment (measured as β/α) and the strength of the incompatibility (measured as γ/α). In the intermediate parameter range (open area), both mechanisms contribute and we see a stepwise transition for various characteristic properties: (1) decrease/increase of population differentiation with increasing recombination rate for weak migration (left/right of dashed line) and (2) decrease/U-shape or increase of $m_{\text{max}}^{+}$ with increasing recombination rate (left/right of dotted line).

Figure 3

Maximum migration rates as functions of the (scaled) strength of epistasis for the haploid (A1–A3), recessive diploid (B1–B3), and codominant diploid (C1–C3) models and for various recombination rates. Each panel represents a different environmental scenario determined by β. For the haploid model, all curves are determined analytically using the formulas in Appendix, Internal equilibria and local stability. See main text for a detailed discussion of this figure and File S4 for interactive visualization of other parameter values.

Figure 4

Maximum migration rate (solid lines) and population differentiation (shaded areas) in the recessive and codominant diploid models as a function of the recombination rate γ. For each model, two choices for the strength γ of epistasis (weak/strong) and three choices for β, describing different types of selection scenarios (corresponding to local adaptation/heterogeneous/homogeneous environments), are represented. Similar to the haploid model (cf. Figure 1), the results in the recessive model are almost independent of the strength of epistasis (compare A1–A3 and B1–B3), but strongly dependent on the environment (compare rows 1, 2, and 3). In contrast, for the codominant model, $m_{\text{max}}^{+}$ and $m_{\text{max}}^{-}$ depend only weakly on the environment if epistasis is strong (D1–D3). Generally, the codominant model produces stronger population differentiation than the recessive model (dark shading dominating), although the overall maximum migration rate in scenarios of local adaptation is lower; compare A1 and B1 with C1 and D1.

Figure A1

State-space diagram, projected onto the plane spanned by the allele frequencies p and q, showing the possible equilibria and initial states of the haploid dynamics. Immigration of continental haplotypes moves the monomorphic equilibrium M₃ (which exists for m = 0) into the interior of the state space, thus yielding a stable DMI. Open circles represent instable equilibria, whereas half-filled circles represent equilibria which can be stable or instable. The gray circle represents a potential polymorphic initial state.