Universal features of correlated bursty behaviour

Abstract

Inhomogeneous temporal processes, like those appearing in human communications, neuron spike trains, and seismic signals, consist of high-activity bursty intervals alternating with long low-activity periods. In recent studies such bursty behavior has been characterized by a fat-tailed inter-event time distribution, while temporal correlations were measured by the autocorrelation function. However, these characteristic functions are not capable to fully characterize temporally correlated heterogenous behavior. Here we show that the distribution of the number of events in a bursty period serves as a good indicator of the dependencies, leading to the universal observation of power-law distribution for a broad class of phenomena. We find that the correlations in these quite different systems can be commonly interpreted by memory effects and described by a simple phenomenological model, which displays temporal behavior qualitatively similar to that in real systems.

Figure 1. Activity of single entities with color-coded inter-event times.

(a): Sequence of earthquakes with magnitude larger than two at a single location (South of Chishima Island, 8th–9th October 1994) (b): Firing sequence of a single neuron (from rat's hippocampal) (c): Outgoing mobile phone call sequence of an individual. Shorter the time between the consecutive events darker the color.

Figure 2. The characteristic functions of human communication event sequences.

The P(E) distributions with various Δt time-window sizes (main panels), P(t_ie) distributions (left bottom panels) and average autocorrelation functions (right bottom panels) calculated for different communication datasets. (a) Mobile-call dataset: the scale-invariant behavior was characterized by power-law functions with exponent values , and (b) Almost the same exponents were estimated for short message sequences taking values , and . (c) Email event sequence with estimated exponents , and . A gap in the tail of A(τ) on figure (c) appears due to logarithmic binning and slightly negative correlation values. Empty symbols assign the corresponding calculation results on independent sequences. Lanes labeled with s, m, h and d are denoting seconds, minutes, hours and days respectively.

Figure 3. The characteristic functions of event sequences of natural phenomena.

The P(E) distributions of correlated event numbers with various Δt time-window sizes (main panels), P(t_ie) distributions (right top panels) and average autocorrelation functions (right bottom panels). (a) One station records of Japanese earthquake sequences from 1985 to 1998. The functional behavior is characterized by the fitted power-law functions with corresponding exponents , and . Inter-event times for P(t_ie) were counted with 10 second resolution. (b) Firing sequences of single neurons with 2 millisecond resolution. The corresponding exponents take values as , and . Empty symbols assign the calculation results on independent sequences. Lanes labeled with ms, s, m, h, d and w are denoting milliseconds, seconds, minutes, hours, days and weeks respectively.

Figure 4. Empirical and fitted memory functions of the mobile call sequence (a) Memory function calculated from the mobile call sequence using different Δt time windows.

(b) 1−p(n) complement of the memory function measured from the mobile call sequence with Δt = 600 second and fitted with the analytical curve defined in equation (4) with ν = 2.971. Grey symbols are the original points, while black symbols denotes the same function after logarithmic binning. (c) P(E) distributions measured in real and in modeled event sequences.

Figure 5. Schematic definition and numerical results of the model study.

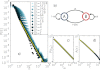
(a) P(E) distributions of the synthetic sequence after logarithmic binning with window sizes Δt = 1…1024. The fitted power-law function has an exponent β = 3.0. (b) Transition probabilities of the reinforcement model with memory. (c) Logarithmic binned inter-event time distribution of the simulated process with a maximum interevent time . The corresponding exponent value is γ = 1.3. (d) The average logarithmic binned autocorrelation function with a maximum lag τ^max = 10⁴. The function can be characterized by an exponent α = 0.7. Simulation results averaged over 1000 independent realizations with parameters µ_A = 0.3, µ_B = 5.0, ν = 2.0, π = 0.1 and T = 10⁹. For the calculation we chose the maximum inter-event time , which is large enough not to influence short temporal behavior, but it increases the program performance considerably.