Simple model of hydrophobic hydration

Abstract

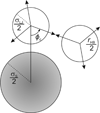
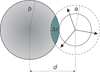
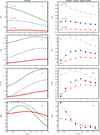
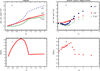
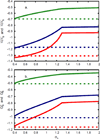
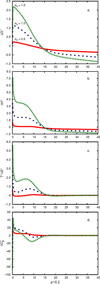
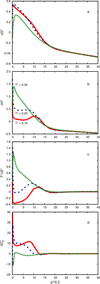
Water is an unusual liquid in its solvation properties. Here, we model the process of transferring a nonpolar solute into water. Our goal was to capture the physical balance between water's hydrogen bonding and van der Waals interactions in a model that is simple enough to be nearly analytical and not heavily computational. We develop a 2-dimensional Mercedes-Benz-like model of water with which we compute the free energy, enthalpy, entropy, and the heat capacity of transfer as a function of temperature, pressure, and solute size. As validation, we find that this model gives the same trends as Monte Carlo simulations of the underlying 2D model and gives qualitative agreement with experiments. The advantages of this model are that it gives simple insights and that computational time is negligible. It may provide a useful starting point for developing more efficient and more realistic 3D models of aqueous solvation.

FIGURE 1

Three states of interaction between Mercedes–Benz model water molecules. Panels: (a) test water makes a hydrogen bond with its neighbor, (b) test water makes a van der Waals contact with its neighbor, (c) test water forms no interaction with its neighbor.

FIGURE 2

Definition of the critical angle ϕ_c.

FIGURE 3

Schematic representation of the overlap volume, Δυ (green shaded area), calculated via equation (26). It equals the intercept volume of the solute’s volume (left circle) and the molar volume of the bulk water, ${\upsilon }_{\text{mol}}^{\mathrm{b}}$ (right dashed circle).

FIGURE 4

Temperature trends in the transfer thermodynamics. Panels (a, b, c, d) are theoretical predictions, panels (e, f, g, h) are Monte Carlo results for a simple Lennard–Jones solute in Mercedes–Benz water (line is plotted as a guide for the eye). Solute radii are: σ_s = 0.5 (red; continuous line, ●), 1.0 (blue; dashed line, ■), and 1.5 (green; dash-dotted line, ▲). Temperatures are scaled to the temperature where the entropy of transfer of a solute of size 0.7 equals zero: theory, $T_{\mathrm{t}}^{*}=0.200$; simulation, $T_{\mathrm{s}}^{*}=0.236$. Pressure is set to p* = 0.19. On panel (h) data for σ_s = 1.5 were omitted due to bad sampling statistics.

FIGURE 5

Experimental temperature trends in the transfer thermodynamics of argon at 1 atm. Panel (a): ΔG (continuous line, ●), ΔH (dashed line, ■), and TΔS (dash-dotted line, ▲). Panel (b): ΔC_p. Data are taken from Ref. , line is plotted as a guide for the eye.

FIGURE 6

Size dependence of the thermodynamic functions. Panels (a, b): ΔG* (red; continuous line, ●), ΔH* (blue; dashed line, ■), T*ΔS* (green; dash-dotted line, ▲) as a function of the solute radius, σ_s. Panels (c, d): $\mathrm{\Delta }{C}_p^{*}/{\sigma }_{\mathrm{s}}$ vs σ_s. Panels (a) and (c) show predictions of the theory for T* = 0.2, p* = 0.19, while data on panels (b) and (d) are simulation results, taken from Ref. and apply for T* = 0.18.

FIGURE 7

Angular distribution W for first-shell waters around a hydrophobic solute of size σ_s = 0.5 (red; continuous line), 1.0 (blue; dashed line), and 4.0 (green; dash-dotted line). Panel (a): theory, $T^{*}=T_{\mathrm{t}}^{*}=0.200$; panel (b): simulation, $T^{*}=T_{\mathrm{s}}^{*}=0.236$. p* = 0.19. Inset in panel (a) schematically defines the angle.

FIGURE 8

Size dependence of (a) the average energy of a water molecule in the first solvation shell (continuous lines), $\overline{{\langle \epsilon \rangle }_{\mathrm{h}}}$, and the value of the average energy, $\overline{{\langle \epsilon \rangle }_{\mathrm{b}}}$, in the bulk (dashed lines), and (b) same for the Gibbs free energy of a water molecule. Results are at different temperatures: T* = 0.16 (red), 0.20 (blue), and 0.30 (green). Pressure is set to p* = 0.19.

FIGURE 9

Pressure dependence of the (a) Gibbs free energy, (b) enthalpy, (c) entropy, and (d) heat capacity of transfer of a simple Lennard–Jones solute into Mercedes–Benz like water. Solute radii are: σ_s = 0.5 (red; continuous line), 1.0 (blue; dashed line), and 1.5 (green; dash-dotted line). Temperature is set to T* = 0.2.

FIGURE 10

Same as in Figure. 9. Temperatures are: T* = 0.16 (red; continuous line), 0.2 (blue; dashed line), and 0.3 (green; dash-dotted line). Solute radius is σ_s = 0.7.